Trisecting a paper using hand and without using a ruler or compass

Question

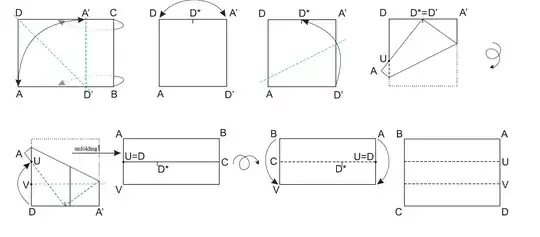
This is a practical problem born while folding a paper.

We can bisect a paper by using only hand.

$\star$ Easy, fold it so that the two ends (of the length) coincide and press the paper to get the bisector of the length.

Repeating the $\star$ again and again we can divide the paper into $2^n$ (where $n\in\mathbb{N}$) parts using only hand.

But how can we divide the paper into some other(I mean other than $2^n$) number of parts .And particularly,

How can we divide the paper into three parts? Using only hand and instruments like ruler, compass, protractor etc and cutting away any piece of paper is banned.

I would recommend the reader to take a paper and try it!, it's really interesting!.

You can find a couple of solutions here, at the Wu::Riddles forum. — Karl Kroningfeld, May 03 '13 at 09:17

ulead86 · Accepted Answer · 2013-05-03T09:36:52.053

6

Try this to get three equal parts

enter image description here

edited May 03 '13 at 09:36

answered May 03 '13 at 09:08

ulead86

3,441

1

This won't give you $3$ equal parts. The two end parts will be $3/8$th of the page and the middle part will be $1/4$. – EuYu May 03 '13 at 09:15
Thanks a lot, I edited my post – ulead86 May 03 '13 at 09:37

Trisecting a paper using hand and without using a ruler or compass

1 Answers1