Chi Squared for Goodness of Fit

Question

Hi, any help is appreciated :)

I am trying to teach myself statistics. I've watched the Khan Academy Series on Chi square statistic for hypothesis testing (https://www.khanacademy.org/math/ap-statistics/chi-square-tests/chi-square-goodness-fit/v/chi-square-statistic)

After completing the multiple choice quizzes, I wanted to create an example of a usecase from my field and walk through the calculating chi square and determining goodness of fit.

Here's the assignment I made for myself:

1. Description of scenario

Education manager has historical enrollment data, showing the final student enrollment statuses on average are:

5% - transfer

10% - withdraw

20% - fail

65% - pass

Over the past two years, there have been organizational changes, so the manager wants to see if the seemingly improved pass rates are better than what we might expect by random chance, given the known distribution.

2. Sample Size, Does it pass the large counts condition?

Sample size will be 100, since that is the smallest sample that allows the expected count of 5 or higher.

3. Observed Counts (statistic)

transfer - 1 (1.6)

withdraw - 5 (2.5)

fail - 10 (5)

pass - 84 (5.55)

4. Chi Square Test Statistic

$\chi ^{2} = 14.65$

5. Test of Significance

df = 3

$\alpha = 0.05$

critical value = 7.815

$\chi ^{2} = 14.65 > 7.815$

So, the difference between the observed and expected values is significant

P-Value

$H_0 =$ the sample is from the distribution

$H_a =$ the sample is from a different distribution

$P = 0.002 < P=0.05$

6. Conclusion

Reject the null hypothesis. The observed scores are not from the same distribution. In plain speak, the differences that I am seeing in enrollment trends are significant.

Thank you

Answer 1

In your computation, you must use observed counts and expected counts (not proportions). In R:

obs=c(1,5,10,84); exp=c(.05,.1,.2,.65)*100
rbind(obs, exp)
    [,1] [,2] [,3] [,4]
obs    1    5   10   84
exp    5   10   20   65

I will compute the chis-squared test statistic directly, using a R as a calculator:

$$Q = \sum_{i=1}^4 \frac{(X_i-E_i)^2}{E_i} = 16.25.$$

q = sum((obs-exp)^2/exp); q
[1] 16.25385

Now, using probability functions in R, we find the critical value and the P-value:

c = qchisq(.95, 3);  c
[1] 7.814728
pv = 1-pchisq(16.254, 3);  pv
[1] 0.001005798

The model upon which the expected counts were based is rejected at the 5% level, (a) because $Q = 16.254 \ge 7.815,$ and (b) because the P-value $0.0010 \le 0.05.$

Notes: (1) In order to use R procedures, you need to read the R documentation for 'built-in' test procedures carefully, to make sure you enter data in in exactly the correct format.

For example, the R procedure chisq.test requires a vector of observed counts obs and (at parameter p) a probability vector summing exactly to $1.$ In terms of my Answer above, this can be exp/100. (This is the essence of @AntoniParellada's earlier comment.)

chisq.test(obs, p=exp/100)
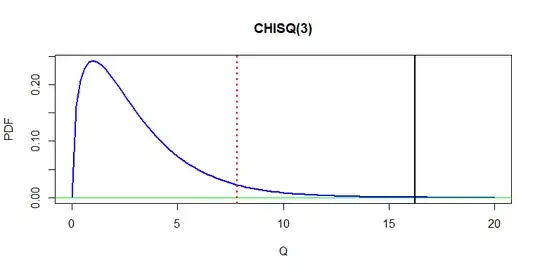
    Chi-squared test for given probabilities


data:  obs
X-squared = 16.254, df = 3, p-value = 0.001006

(2) The figure below shows the density curve of $\mathsf{Chisq}(\nu=3).$ The critical value is denoted by a vertical red dotted line. The area under the density curve to the right of this line is $0.05.$ The vertical black solid line shows the value of the chi-squared test statistic. The P-value of the test is the (very small) area under the density curve to the right of this line.

curve(dchisq(x,3), 0,20, ylab="PDF", xlab="Q",  
      col="blue", lwd=2, main="CHISQ(3)")
 abline(h=0, col="green2")
 abline(v=7.815, col="red", lty="dotted", lwd=2)
 abline(v = 16.25, lwd=2)