With the rise of factory games like Satisfactory and Factorio, many people have started wondering about problems like these.
Factorio already has a very interesting analysis of conveyor dynamics on this question: Belt Balancer problem (Factorio)
As so I will be focusing on a particular problem that shows up in the game Satisfactory.
The key ideia is:
Having a conveyor belt with a known flow of items per second, how to split it into multiple belts, possibly with different flow rates?
On Satisfactory the allowed operations are:
- Splitting a belt in 2 -> 2 new belts, each with 1/2 the flow rate
- Splitting a belt in 3 -> 3 new belts, each with 1/3 the flow rate
- Merging several belts into one.
This set of rules allows for a split belt to be merged into the source stream of the splitter, creating feedback loops that converge into a specific distribution, as shown here. This graphic was brought to my attention on a similar question, trying to solve a particular case of this problem: How do I get 1/15 of something, only by divide with 2 or 3 and add the result back together?
This youtube video also shows solutions for several particular cases of this problem.
While my math skills aren't very good, my ambition certainly is. I would like to see a general solution for this problem, and turn into into a calculator program (because my programming is better than my math).
The objectives of this question are:
- Obtain a proof that it is possible to take one input conveyor with any flow rate and turn it into any number of output conveyors, with any flow rates (outputs can have different flow rates). Or figure out which combinations are impossible.
- Create a general solution / algorithm to solve this problem:
- Given an initial flow rate $X$ which operations need to be applied so that a specified output can be achieved? The most general case would be to allow any number of conveyors, each with any possible flow rate. (Order of conveyors does not matter, we only need to specify how many with what flow rate)
- To put in more "mathy" terms, the inputs to this would be:
- The input flow rate $X$
- A specification of how many conveyors are desired with which flow rate: $n_1$ conveyors with $F_1$ flow rate, $n_2$ conveyors with $F_2$ flow rate, all the way to the $n^{th}$ row $$ \left( \begin{matrix} n_1 & F_1 \\ n_2 & F_2 \\ ... & ...\\ n_n & F_n \end{matrix} \right) $$ This matrix can have any number of rows but $$n_1, ..., n_2 \in \mathbb{N}$$ As the left column values are counters for the number of output conveyors, and $$\sum_{i=1}^{n} n_i F_i = X$$ As the sum of all flow rates of all conveyors must equal que initial flow rate.
With this, the general solution should provide a way to figure out the tree of operations that need to be applied to the initial conveyor to achieve the end result, i.e.
+------------------------------------+---------------------------+ | Operations | Conveyors | +------------------------------------+---------------------------+ | split initial in 3 | X/3 | X/3 | X/3 | | split one of the 10/3 in 2 | x/3 | X/3 | X/6 | X/6 | | merge one of the 10/6 with initial | X/3 | X/3 | X/6 | +------------------------------------+---------------------------+
It is my impression that the feedback and convergence complicate this quite a bit, and it would be best solved numerically, by coming up with a programmable algorithm and having the computer figure it out, finding convergence iteratively and proposing a solution.
Here I am only interested in the operations, leaving it up to the engineer to implement the system in-game, and that is why I have not specified conveyor flow rate limits or other limits related with the physical reality inside the game.
This is a problem that has boggled me for quite some time and I have put considerable effort in preparing this question. Even we never come to a perfect solution I would most certainly like to hear your thoughts and opinions on how to tackle this!
Also I'm not sure how to tag this question as I don't know which fields of mathematics this problem is related to - suggestions accepted.
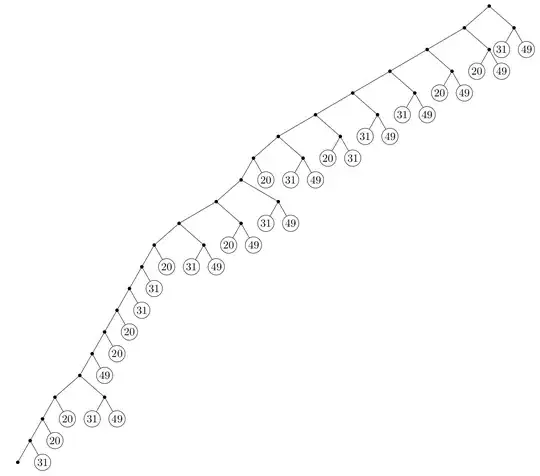
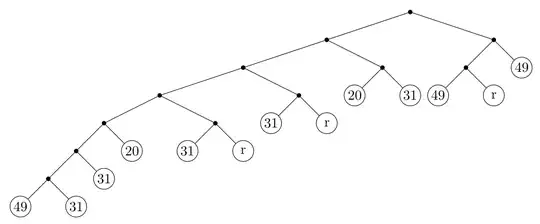
The idea of the second paragraph is that if I take any integer N, to divide a stream into N equal conveyors, all it takes is to find the smallest multiple of 3 (or 2) above N (let's call it X) and feed X-N conveyors back into the input correct? If so this doesn't hit me like the optimal solution as a large number of splitters and mergers would be required. Ideas?
– rosaqq Nov 24 '20 at 12:43