Calculating the P-value of a T-distribution.

Question

Learning some statistics here and in the chapter of Linear Regression I wanted to prove the values that I get on summary() from a created model.

My summary() output is:

Call:
lm(formula = Price ~ Taxes + Size, data = HousePrices)
Residuals:
    Min      1Q  Median      3Q     Max 
-188027  -26138     347   22944  200114
Coefficients:
              Estimate Std. Error t value Pr(>|t|)

(Intercept) -28608.744  13519.096  -2.116   0.0369 *

Taxes           39.601      6.917   5.725 1.16e-07 ***
Size            66.512     12.817   5.189 1.16e-06 ***

Signif. codes:  0 ‘*’ 0.001 ‘’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 48830 on 97 degrees of freedom
Multiple R-squared:  0.7722,    Adjusted R-squared:  0.7675 
F-statistic: 164.4 on 2 and 97 DF,  p-value: < 2.2e-16

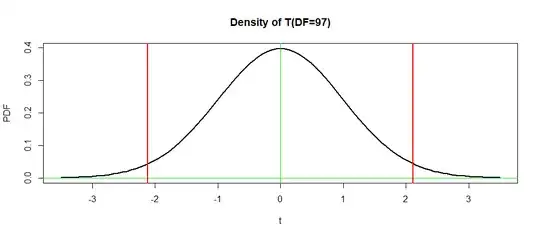
For example to calculate the t-value for the intercept I do

t-value = -28608.744 / 13519.096 = -2.116173

Now I found in other forums that to get the p-value from this H0 I have to find the probability of the tvalue in a lower tail, I do it with the next command.

pvalue1 =  pt(-abs(tvalue), 97, lower.tail = T)*2

I get the right value but I got two questions I cant understand.

Why do I have to calculate the probability always with a negative value of a t-value?
What is the reason to make it with lower tail and then multiply the result by 2?

By symmetry of the $t$-distribution we have$$\mathbb{P}(|T|\gt |t|)=2\cdot\mathbb{P}(T\lt -|t|)=2\cdot\mathbb{P}(T\gt |t|)$$ — Peter Foreman, Jun 13 '20 at 16:28

BruceET · Answer 1 · 2020-06-14T06:08:51.487

Notice the P-value notation is Pr(>|t|), which means $P(T < -t) + P(T > t),$ where $t$ is the computed value of the t statistic, which for 'Intercept' is $t = -2.116$ and the random variable $T \sim \mathsf{T}(\nu=97),$ Student's t distribution with 97 degrees of freedom.

This is for a 2-sided test so we need to find the probability of a result farther from $0$ in either direction than $-2.116.$

In R, the function pt denotes the CDF of a t distribution. So $P(T < -2.116) = P(T \le -2.116) = 0.0184527$ is found as as follows:

pt(-2.116,97)
[1] 0.0184527

And by symmetry of t distributions $P(T > 2.116)$ has the same value. So the total desired probability $0.0369054$ is found in R as follows:

pt(-2.116,97)*2
[1] 0.0369054

In the printout, this is rounded to $0.0369.$

Below, is a graph of the density function of $\mathsf{T}(\nu = 97).$ The vertical red lines are at $\pm 2.116.$ The P-value corresponds to the area under the curve outside of the vertical lines in both tails.

curve(dt(x, 97), -3.5, 3.5, lwd=2, 
    ylab="PDF", xlab="t", main="Density of T(DF=97)")
  abline(h=0, col="green2")
  abline(v=0, col="green2")
  abline(v = c(-2.116,2.116), col="red", lwd=2)

Note: Here are two other methods by which you would get the 2-sided P-value using R. Maybe you can figure out how the R code works in both of them.

pt(-2.116, 97) + pt(2.116, 97, lower.tail=F)
[1] 0.0369054  # add two tails
1 - diff(pt(c(-2.116, 2.116), 97))
[1] 0.0369054  # subtract middle from whole

Calculating the P-value of a T-distribution.

1 Answers1