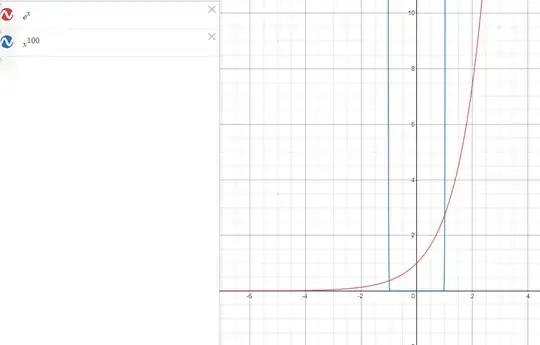
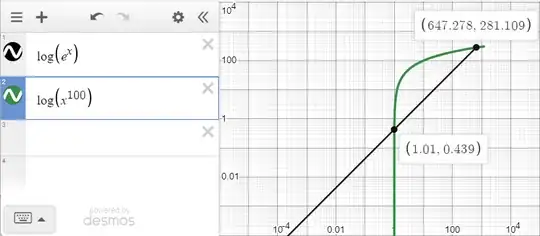
Please see the graphs below.
From here we can see clearly that $x^{100}$ grows faster than $e^x$.
I zoomed out and checked up to $y=5000$ and the result is the same.
But I know that the growth of an exponential function is mathematically proven to be faster than any polynomial function.
Why? What does that phrase actually mean?
Take $x=1000$ which gives $$x^{100}=1.00 \times10^{300} \qquad \text{and} \qquad e^{x}=1.97 \times 10^{434}$$
In fact $e^x > x^{100}$ if $x > 648$.
Redo your plot on a log scale.
Edit
In fact, we can show that, for any real $a$, $e^x > x^a$ as soon as $$x > x_*= -a\, W_{-1}\left(-\frac{1}{a}\right)$$ where appears the second branch of Lambert function.
As a shortcut, $x_* \sim 1.05 \,a \log (a \log (a))$
You just haven't zoomed out enough. If you check say, $x = 1000$, then $e^x > x^{100}$. This is easily verifiable as $$e^{1000} = (e^{10})^{100} > 1000^{100}$$ as $e^{10} > 2^{10} = 1024> 1000$. From there, you can use many ways (comparing ratios, taking derivatives, etc.) to show that $x^{100}$ never catches up.
$e^x$ will be unconditionally greater than $x^a$ for $a < e$. Otherwise there will be a region (as you almost saw) where $e^x$ drops below $x^a$ before becoming unconditionally greater. That critical value was given in the answer by Claude Leibovici.
If you plot $log(e^x)$ and $log(x^100)$ on log-log scales then the region in which one is greater than the other is more clearly seen:
If you compare $e^x$ to $1 + x^a$ (since both start at 1 for $x = 0$) the behavior is similar, but the critical value of $a$ (past which $e^x$ might be less than $x^a$) is $a=2.6327483384777...$, a little bit smaller than $e$.
