Is it impossible to perfectly fit a polynomial to a trigonometric function on a closed interval?

Question

On a closed interval (e.g. $[-\pi, \pi]$), $\cos{x}$ has finitely many zeros. Thus I wonder if we could fit a finite degree polynomial $p:\mathbb{R} \to \mathbb{R}$ perfectly to $\cos{x}$ on a closed interval such as $[-\pi, \pi]$.

The Taylor series is

$$\cos{x} = \sum_{i=0}^{\infty} (-1)^i\frac{x^{2i}}{(2i)!} = 1 - \frac{x^2}{2} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!}-\dots$$

Using Desmos to graph $\cos{x}$ and $1-\frac{x^2}{2}$ yields:

which is clearly imperfect on $[-\pi,\pi]$. Using a degree 8 polynomial (the first 5 terms of the Taylor series above) looks more promising:

But upon zooming in very closely, the approximation is still imperfect:

There is no finite degree polynomial that equals $\cos{x}$ on all of $\mathbb{R}$ (although I do not know how to prove this either), but can we prove that no finite degree polynomial can perfectly equal $\cos{x}$ on any closed interval $[a,b]\subseteq \mathbb{R}$? Would it be as simple as proving that the remainder term in Taylor's Theorem cannot equal 0? But this would only prove that no Taylor polynomial can perfectly fit $\cos{x}$ on a closed interval...

Answer 1

Yes, it is impossible.

Pick any point in the interior of the interval, and any polynomial. If you differentiate the polynomial repeatedly at that point, you will eventually get only zeroes. This doesn't happen for the cosine function, which instead repeats in an infinite cycle of length $4$. Thus the cosine function cannot be a polynomial on a domain with non-empty interior.

Answer 2

We don't even need to differentiate many times. Just note that $f'' = -f$ is satisfied by $f = \cos$ but not if $f$ is a non-zero polynomial function because $f''$ has lower degree than $f$. (This implicitly uses the fact that two polynomials that are equal at infinitely many points must be identical.) $ \def\lfrac#1#2{{\large\frac{#1}{#2}}} $

To answer a comment on Claude's post, here is a neat proof. Define $\deg(\lfrac{g}{h}) = \deg(g)-\deg(h)$ for any polynomial functions $g,h$. Given any function $f = \lfrac{g}{h}$ where $g,h$ are polynomial functions on some non-trivial interval, we have $f' = \lfrac{g'}{h}-\lfrac{g·h'}{h^2} = f·\lfrac{g'·h-g·h'}{g·h}$, and hence $\deg(f') < \deg(f) $ since $\deg(g'·h-g·h') < \deg(g·h)$. Thus $\deg(f'') < \deg(f)$ and therefore $f'' ≠ -f$. So even Padé approximants are not enough to perfectly fit anything except rational functions, on any non-trivial interval.

Answer 3

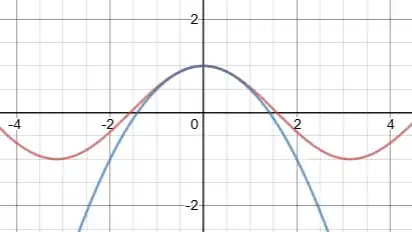
Here's a proof using only basic trigonometry and algebra, no calculus or infinite series required.

We'll do a proof by contradiction. Suppose $\cos(x)$ is a polynomial on some closed interval $[a,b]$, with $a\ne b$. We'll split it into two cases, depending on whether or not $0\in [a,b]$.

Case 1. Suppose your interval contains the origin, i.e. $a \le 0 \le b$. If $\cos(x)$ is a polynomial function on $[a,b]$, then $2\cos^2(\frac x 2) - 1$ is also a polynomial function on $[a,b]$, since $x\in[a,b]$ implies $x/2 \in [a,b]$. Now, recall the half angle formula for $\cos(x)$:$$ \cos(x) = 2\cos^2(\frac x 2) - 1 $$ The half-angle formula tells us that these two polynomials are in fact the same polynomial. But if $\cos(x)$ has degree $n$, then $2\cos^2(\frac x 2) - 1$ must have degree $2n$. Since two polynomials with different degree cannot be equal on any interval, this implies $2n = n$, or $n=0$. Since $\cos(x)$ is not constant, we have a contradiction, so $\cos(x)$ is not a polynomial on any interval containing $0$.

Case 2. Now, what if the interval does not contain the origin? This takes a few more steps, but we can show that if $\cos(x)$ is a polynomial on $[a,b]$, then it must also be a polynomial (potentially a different polynomial) on $[0,b-a]$, which contains the origin so is impossible by the above argument.

For $x\in [0,b-a]$, we use the angle sum formula to find $$ \cos(x) = \cos(x+a -a) = \cos(x+a)\cos(a) + \sin(x+a)\sin(a) $$ Since $\cos(x+a)$ is a polynomial of $x$, and $\sin(x+a)^2 + \cos(x+a)^2= 1$, this means that on the interval $[0,b-a]$, the cosine of $x$ has the property that $$ \left(\cos(x) - p(x)\right)^2 = q(x) $$ for some polynomials $p$ and $q$. In particular $p(x) = \cos(a+x)\cos(a)$ and $q(x) = \sin^2(a) \left(1-\cos^2(x+a)\right)$. Equivalently, $\cos(x) = p(x) \pm \sqrt{q(x)}$. Again, the half-angle formula tells us $\cos x = 2\cos^2(\frac x 2) - 1$ (for $x\in[0,b-a]$). Substituting into the above, we get some very messy algebra:\begin{eqnarray} \left(2\cos^2\left(\frac x 2\right) - 1 - p(x)\right)^2 &=& q(x)\\ \left(2p(\frac x 2)^2 \pm 4 p(\frac x 2)\sqrt{q(\frac x 2)} + 2q(\frac x 2) - 1 - p(x)\right)^2 &=& q(x)\end{eqnarray} expanding the left-hand side, we get:$$ q(x) = \left(2p(\frac x 2)^2+ 2q(\frac x 2) - 1 - p(x)\right)^2 + 16 p(\frac x 2)^2q(\frac x 2) \pm 8\left(2p(\frac x 2)^2+ 2q(\frac x 2) - 1 - p(x)\right)p(\frac x 2)\sqrt{q(\frac x 2)} $$ which implies $\pm\sqrt{q(x/2)}$ is actually a rational function. Since its square is a polynomial, this means $\pm\sqrt{q(x/2)}$ is a polynomial itself, so $\pm\sqrt{q(x)}$ is also a polynomial. Therefore $\cos(x) = p(x) \pm \sqrt{q(x)}$ is a polynomial for $x\in[0,b-a]$. Since this interval contains the origin, we again have a contradiction, so $\cos(x)$ cannot be a polynomial on $[a,b]$.

All this shows why results from calculus are helpful - the problem is trivial if we bring in derivatives!

---

As an addendum: All of these arguments can be generalized to show that $\cos(x)$ is also not a rational function on any interval, and that the other trig functions similarly are not polynomials or rational functions.

Answer 4

If $p$ is a polynomial the function $f(z) = p(z)-\cos z$ is entire, and the uniqueness theorem shows that if $f(z) = 0$ on any line segment then $f= 0$.

(The uniqueness theorem is stronger than that, it just needs $f$ to be zero on any sequence with an accumulation point.)

Addendum:

To clarify, since a non zero polynomial has at most $\partial p$ zeros and $\cos$ has a countable number then we cannot have $f=0$.

Answer 5

I do not know if you have any specific reason to require a polynomial.

Nevertheless, for function approximations, Padé approximants are much better than Taylor expansions even if, to some extent, they look similar. For example $$\cos(x) \sim \frac {1-\frac{115 }{252}x^2+\frac{313 }{15120}x^4 } {1+\frac{11 }{252}x^2+\frac{13 }{15120}x^4 }$$ is better than the Taylor series to $O(x^{9})$ that you considered

To compare $$\int_{-\pi}^\pi \Big[ \frac {1-\frac{115 }{252}x^2+\frac{313 }{15120}x^4 } {1+\frac{11 }{252}x^2+\frac{13 }{15120}x^4 }-\cos(x)\Big]^2\,dx=0.000108$$ $$\int_{-\pi}^\pi \Big[1-\frac{x^2}{2}+\frac{x^4}{24}-\frac{x^6}{720}+\frac{x^8}{40320}-\cos(x)\Big]^2\,dx=0.000174$$ but nothing is absolutely perfect.

If I add one more term to the Padé approximant, the values of the corresponding integral become $1.25\times 10^{-9}$ and for $x=\frac \pi 2$ the value of the approximated function is $-6.57\times 10^{-9}$.

Now, have a look at an approximation I built for you $$\cos(x)=\frac{1-\frac{399 }{881}x^2+\frac{20 }{1037}x^4 } {1+\frac{58 }{1237}x^2+\frac{1}{756}x^4 }$$ which gives for the integral $1.49\times 10^{-8}$.

Answer 6

One of the statements you mentioned you don't know how to prove, is easy. $\cos x$ has infinitely many roots along the real line but any polynomial of finite degree would have finitely many roots. But, there cannot be a finite degree polynomial that equals $\cos x$ on $[-\pi, \pi]$ or any other closed interval, for that matter. You could show that the power series you provided for $\cos x$ converges uniformly on any closed interval. So, if $\cos x = p(x)$ for some finite degree polynomial, $p(x)$ could also be viewed as a power series with finitely many non zero coefficients. But, the power series of a function (assuming convergence) is unique. Hence, such $p$ cannot exist. However, you could approximate $\cos x$ with polynomials within any precision that you would like, by the Stone Weierstrass theorem.

Answer 7

No, it is not impossible, but only for the reason that a single point is a closed interval. You can certainly get exact agreement between cosine and a polynomial on any closed interval, $[p,p]$, $p \in \Bbb{R}$. If the closed interval you are interested in has nonempty interior, then, yes, it is impossible (as adequately explained elsewhere).

Answer 8

Given a smooth function on an interval and an interior point of that interval, the Taylor series of that function around the point is completely determined. Then you are looking for a polynomial whose Taylor series around $0$ (say) coincides with that of the cosine, which obviously does not exist, since any polynomial is its own Taylor series.

Of course if you consider a single point to be a closed interval, then a perfect approximation on that interval is possible.

Answer 9

Altho other people have already mentioned the impossibility of having a polynomial that is everywhere equal to the cosine over a finite interval, for a smooth function like cosine, it is possible to obtain a uniform approximation that can be made as close an approximation as possible. This involves an expansion in terms of Chebyshev polynomials (of the first kind), and in fact there is an entire project, the Chebfun project, that relies on approximating complicated functions as (possibly piecewise) Chebyshev series.

I will give a concrete example in Mathematica (adapted from this answer). In the following, I have arbitrarily chosen a polynomial approximation of degree $128$ to approximate the cosine:

f[x_] := Cos[x];
{a, b} = {-π, π}; (* interval of approximation *)
n = 128; (* arbitrarily chosen integer *)
prec = 25; (* precision *)
cnodes = Rescale[N[Cos[π Range[0, n]/n], prec], {-1, 1}, {a, b}];
fc = f /@ cnodes;
cc = Sqrt[2/n] FourierDCT[fc, 1];
cc[[{1, -1}]] /= 2;

cosApprox[x_] = cc.ChebyshevT[Range[0, n], Rescale[x, {a, b}, {-1, 1}]]

{Plot[{f[x], cosApprox[x]}, {x, a, b},
      PlotLegends -> Placed[{"Exact", "Chebyshev series"}, Bottom],
      PlotStyle -> {AbsoluteThickness[4], AbsoluteThickness[1]}],
 Plot[f[x] - cosApprox[x], {x, a, b},
      PlotRange -> All, PlotStyle -> ColorData[97, 4]]} // GraphicsRow

In theory, as you increase the degree, the approximation gets better and better; in practice, you will often hit the limits of your machine's numerics.

Answer 10

Although this is an incomplete answer unlike the ones I read here, I'd like to offer what I eventually thought of since the idea still seems original: There can be no polynomial with rational coefficients that exactly approximates $\cos$ on $[0,1]$, because it will have a wrong integral over this interval ($\sin 1$ being irrational). I believe this argument can be adapted to a different interval $[\alpha,\beta]$ by finding a sub-interval with rational endpoints $[a,b] \subset [\alpha,\beta]$ and using something like the notion of algebraic independence over $\mathbb{Q}$ (search for $a$ and $b$ such that $\sin b - \sin a$ be irrational? Which should happen most of the time) and/or Niven's theorem, and possibly enhanced to real coefficients since a polynomial with such coefficients can be well-approximated by sequences of polynomials with rational ones. Thank you for your question, it reminds me much of the kind I would've asked when younger!