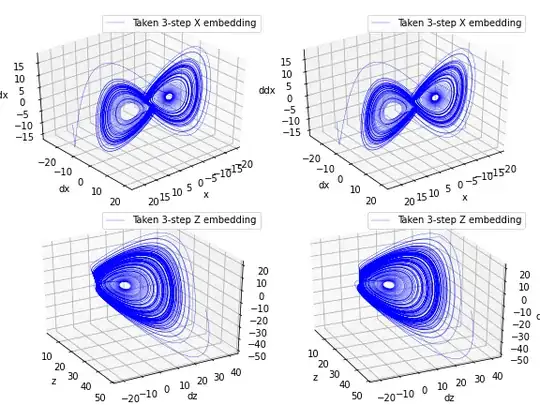
Show that observation of $z$ component alone of the Lorenz equations \begin{align} \dot x& = \sigma (y-x)\\ \dot y &= x (\rho -z) -y\\ \dot z &= xy-\beta z \end{align} does not lead to an embedding. Why does this not violating Takens' Theorem? What modification is required to generate an embedding?
Given the Lorenz equations, how come when I only observe the $z$ component alone i.e: ($\frac{\mathrm{d}z}{\mathrm{d}t} = xy - Bz$), this does not lead to an embedding. By Whitney’s embedding theorem, I need an embedding $Q$ to map from a finite $d$-dimensional attractor $A$ to $\mathbb R^k$ with $k \ge 2d+1$. In this case is $Q$ mapping from 2 dimensions to 1 dimension? Hence $k = 1$, $d = 2$ thus not satisfying $k \ge 2d+1$? How does this not violate Takens’ theorem, which states:
If $A$ is a finite-dimensional manifold and $q : A \to \mathbb R$ is differentiable then $v : A \to \mathbb R^k$ where $k > 2d$ is either an embedding or an arbitrarily small differentiable perturbation of $q$ and/or $\tau$ makes $v$ an embedding.