How does one go about finding the branch points/holomorphic branches of a multi-function composed of several other multi-functions? Here is an example of what I mean:
Let $f(z)= [\frac{\sqrt{z} \log(z)}{(1+z)^2}]$ be a multifunction. Identify the branch points and find a holomorphic branch.
I have no idea how to approach this if $\sqrt{z}$ and $\log(z)$ are considered multi-functions themselves. Can someone help me out here? Thanks!
We have two multi-valued functions $\sqrt{z}$ and $\log{z}$ to consider when looking for branch points of \begin{align*} \frac{\sqrt{z}\log{z}}{(1+z)^2}\tag{1} \end{align*}
We start by looking at each of the functions separately to recall the base information. At first the simpler one:
Branch points of $\sqrt{z}$:
Since $\sqrt{z}$ is the inverse of the function $z^2$ we expect $w(z)=\sqrt{z}$ having two values. To analyse the multivaluedness it is convenient to use polar coordinates and we write $z=re^{i\theta}$ with $\theta=\theta_{p}+2\pi n$ and $0\leq \theta_{p}<2\pi, n\in\mathbb{Z}$. We then have \begin{align*} w=r^{1/2} e^{i\theta_{p}/2}e^{n\pi i}\tag{2} \end{align*} where $r^{1/2}=\sqrt{r}\geq 0$ and $n$ is an integer. For a given value of $z$, the function $w(z)=\sqrt{z}$ takes two possible values corresponding to $n$ even and $n$ odd, namely \begin{align*} \sqrt{r}e^{i\theta_{p}/2}\qquad\text{and}\qquad \sqrt{r}e^{i\theta_{p}/2}e^{\pi i}=-\sqrt{r}e^{i\theta_{p}/2} \end{align*}
The key observation here is, when traversing a small circuit around $z=0$, we do not return to the original value. When starting for instance at $z=\varepsilon$ for real $\varepsilon >0$ and letting $n=0$ we start with $\theta_p=0$ and after returning to $z=\varepsilon, \theta_p=2\pi$ we have according to (2) $w=\sqrt{\varepsilon}e^{2i\pi/2}=-\sqrt{\varepsilon}$. Traversing another circuit we have $w=\sqrt{\varepsilon}e^{4i\pi/2}=\sqrt{\varepsilon}$ and this continues for $n$ even and $n$ odd.
Since a point is a branch point of a function $w(z)$ iff it is discontinuous upon traversing a small circuit around this point, we have $0$ identified as branch point of the function $w(z)=\sqrt{z}$.
The point at $z=\infty$ is another branch point of $\sqrt{z}$ which can be seen as follows. We consider $z=\frac{1}{t}$ and note that $0$ is a branch point of $t^{-1/2}$ which can be argued in the same we as we did above for $z^{1/2}$.
If we take a closed circuit that does not enclose $z=0$ then the phase $\theta_p$ varies continuously between two values $0\leq \theta_1\leq \theta_p\leq \theta_2<2\pi$ as $z$ traverses the circuit returning exactly to its previous value with no phase change.
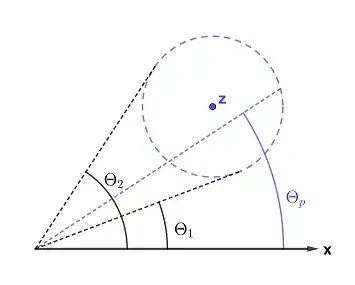
We are now in the situation to restrict $w$ to an open region of the plane so that the resulting function is single-valued and continuous. One way to do so is by taking $n=0$ and restricting the region by cutting out the real positive axis and by also deleting $z=0$ and $z=\infty$. The semiaxis $\Re z>0$ is called the branch cut.
Branch points of $\log{z}$:
Since $\log{z}$ is the inverse of the function $e^z$ which has period $2\pi i$ we expect $w(z)=\log{z}$ having countably infinite values. We use polar coordinates and write $z=re^{i\theta}$ with $\theta=\theta_{p}+2\pi n$ and $0\leq \theta_{p}<2\pi, n\in\mathbb{Z}$. We then have \begin{align*} w=\log{r} + i\theta_{p}+2n\pi i\tag{3} \end{align*} where $\log r> 0$ and $n$ is an integer. For a given value of $z$, the function $w(z)=\log{z}$ takes infinite values corresponding to $n\in\mathbb{Z}$.
Again, when traversing a small circuit around $z=0$, we do not return to the original value. When starting for instance at $z=\varepsilon$ for real $\varepsilon >0$ and letting $n=0$ we start with $\theta_p=0$ and after returning to $z=\varepsilon, \theta_p=2\pi$ we have according to (3) $w=\log{r} + i\theta_{p}+2\pi i$. Traversing another circuit we have $w=\log{r} + i\theta_{p}+4\pi i$ and this continues for $n\in \mathbb{Z}$.
So, we have $0$ identified as branch point of the function $w(z)=\log{z}$.
The point at $z=\infty$ is another branch point of $\log{z}$ which can be seen as follows. We consider $z=\frac{1}{t}$ and note that $0$ is a branch point of $\log{\frac{1}{t}}=-\log{t}$ which can be argued in the same way as we did above for $\log{z}$.
If we take a closed circuit that does not enclose $z=0$ then the phase $\theta_p$ varies continuously between two values $0\leq \theta_1\leq \theta_p\leq \theta_2<2\pi$ as $z$ traverses the circuit returning exactly to its previous value with no phase change.
We are now in a similar situation as with $w=\sqrt{z}$. We have two branch points and can use the same branch cut $\{z|z>0\}$ to restrict $w(z)=\log{z}$ to an open region where $w$ is single-valued and continuous. We might also have cut out the real negative axis with phase angle $\theta_p$ in $(-\pi,\pi]$ and obtain this way the principal value of the logarithm.
Branch points of $\frac{\sqrt{z}\log{z}}{(1+z)^2}$:
We can proceed similarly as we did above. At first we note that it is sufficient to consider $w(z)=\sqrt{z}\log{z}$ since $\frac{1}{(1+z)^2}$ is analytic in $\mathbb{C}\setminus\{-1\}$ and single-valued. In order to analyse the multivaluedness of $w(z)$ we write $z=re^{i\theta}$ with $\theta=\theta_{p}+2\pi n$ and $0\leq \theta_{p}<2\pi, n\in\mathbb{Z}$. We then have \begin{align*} w=r^{1/2} e^{i\theta_{p}/2}e^{n\pi i}(\log{r} + i\theta_{p}+2n\pi i)\tag{4} \end{align*} where $r\geq 0$ and $n$ is an integer. We will see for a given value of $z$, the function $w(z)=\sqrt{z}\log{z}$ takes infinite values corresponding to $n\in\mathbb{Z}$.
Indeed, when traversing a small circuit around $z=0$, we do not return to the original value. When starting for instance at $z=\varepsilon$ for real $\varepsilon >0$ and letting $n=0$ we start with $\theta_p=0$ and after returning to $z=\varepsilon, \theta_p=2\pi$ we have according to (4) $w=\sqrt{\varepsilon}e^{2i\pi/2}\left(\log{r} + 2\pi i\right)=-\sqrt{\varepsilon}\left(\log{r} + 2\pi i\right)$. Traversing another circuit we have $w=\sqrt{\varepsilon}\left(\log{r} + 4\pi i\right)$ and this continues for $n\in \mathbb{Z}$ changing the sign for $n$ even and $n$ odd.
Again, we have $0$ identified as branch point of the function $w(z)=\sqrt{z}\log{z}$.
The point at $z=\infty$ is another branch point of $\sqrt{z}\log{z}$ which can be seen as above by substituting $z=\frac{1}{t}$ and considering $t$ close by $0$ which can be argued in the same way as we did above.
If we take a closed circuit that does not enclose $z=0$ then the phase $\theta_p$ varies continuously between two values $0\leq \theta_1\leq \theta_p\leq \theta_2<2\pi$ as $z$ traverses the circuit returning exactly to its previous value with no phase change.
We are now in a similar situation as with the functions $\sqrt{z}$ and $\log{z}$. We have two branch points $z=0$ and $z=\infty$ and can use the same branch cut $\{z|z>0\}$ to restrict $w(z)=\sqrt{z}\log{z}$ to an open region where $w$ is single-valued and continuous.
Note: This answer follows closely section: 2.2 Multivalued functions from Complex Variables: Introduction and Applications by M.J. Ablowitz and A.S. Fokas.
