Look at the composites between twin primes (A014574):
$$ 4, 6, 12, 18, 30, 42, 60, 72, 102, 108, 138, 150, 180, 192, 198, 228, \\ 240, 270, 282, 312, 348, 420, 432, 462, 522, 570, 600, 618, \ldots \;. $$
Is there anything special about their distribution of factors, number of divisors, or other number-theoretical properties? Or are these twin-prime averages totally "normal" numbers, as far as we know?
This answer is analogous to my answer to Why do even numbers which surround primes have more divisors than those which surround composites?. In order to make it self-contained, I'll repeat some things that I wrote there. I'll derive the expected (additive) excess of distinct prime factors and the expected (multiplicative) excess of divisors of a large even number between twin primes.
On the random model of the primes, the probability for an even number $n$ to be divisible by an odd prime $p$ is a priori $\frac1p$. If we know that $n$ is adjacent to two primes $q$, $q+2$, this is increased to $\frac1{p-2}$, since we know that $q$ and $q+2$ are not divisible by $p$, which excludes two of the non-zero values of $n\bmod p$.
The expected number of distinct prime factors of an even number $n$ is roughly
$$ 1+\sum_{3\le p\le n^r}\frac1p\;, $$
where $r=\mathrm e^\gamma$ (see Asymptotic distance between $x^2+1$ primes?). Conditional on $n$ being between twin primes $q$, $q+2$ this becomes
\begin{eqnarray} 1+\sum_{3\le p\le n^r}\frac1{p-2} &=& 1+\sum_{3\le p\le n^r}\frac1p+\sum_{3\le p\le n^r}\left(\frac1{p-2}-\frac1p\right) \\ &=& 1+\sum_{3\le p\le n^r}\frac1p+\sum_{3\le p\le n^r}\frac2{p(p-2)} \\ &\approx& 1+\sum_{3\le p\le n^r}\frac1p+\sum_{3\le p}\frac2{p(p-2)} \;, \end{eqnarray}
where we can remove the upper limit on the right-hand sum for large $n$ since this series converges (whereas the sum over $\frac1p$ diverges). To improve convergence, we can write
\begin{eqnarray} \sum_{3\le p}\frac2{p(p-2)} &=& 2\sum_{3\le p}\left(\frac1{p^2}+\frac2{p^2(p-2)}\right) \\ &=& 2\left(P(2)-\frac14+2\sum_{3\le p}\frac1{p^2(p-2)}\right)\;, \end{eqnarray}
where $P(s)$ is the Prime zeta function. We have $P(2)\approx0.452247$, and Wolfram|Alpha evaluates the right-hand series to approximately $0.130647$, so the excess in the number of distinct prime factors of a large even number between twin primes comes out as approximately $0.927084$, almost a whole prime factor, and more than three times the excess for large even numbers adjacent to a prime.
We can perform a similar analysis to find the (in this case multiplicative) excess of divisors for even numbers between twin primes. A number with prime factorization $\prod_ip_i^{k_i}$ has $\prod_i(k_i+1)$ divisors, so the logarithm of the number of divisors is $\sum_i\log(k_i+1)$.
For a given odd prime $p$, a priori an even number $n$ has probability $\frac{p-1}p$ of containing $0$ factors of $p$, probability $\frac1p\cdot\frac{p-1}p$ of containing $1$ factor of $p$, and generally probability $\frac1{p^k}\frac{p-1}p$ of containing $k$ factors of $p$. Conditional on $n$ being between twin primes, it has probability $\frac{p-3}{p-2}$ of containing no factors of $p$, probability $\frac1{p-2}\frac{p-1}p$ of containing $1$ factor of $p$, and generally probability $\frac{p-1}{p-2}\frac1{p^k}$ of containing $k\gt0$ factors of $p$.
Thus the expected excess in the logarithm of the number of divisors given that $n$ is between twin primes is
\begin{eqnarray} \sum_{3\le p}\sum_{k=0}^\infty\frac{\log(k+1)}{p^k}\left(\frac{p-1}{p-2}-\frac{p-1}p\right) &=& 2\sum_{3\le p}\sum_{k=0}^\infty\frac{\log(k+1)}{p^{k+1}}\frac{p-1}{p-2} \\ &=& 2\sum_{3\le p}\sum_{k=2}^\infty\frac{\log k}{p^k}\frac{p-1}{p-2}\;. \end{eqnarray}
I don't see a way to rewrite this as a single sum. To improve the convergence of the double sum, we can rewrite it like this:
\begin{eqnarray*} 2\sum_{3\le p}\sum_{k=2}^\infty\frac{\log k}{p^k}\frac{p-1}{p-2} &=& 2\sum_{3\le p}\sum_{k=2}^\infty\left(\frac{\log k}{p^k}+\frac{\log k}{p^k}\frac1{p-2}\right) \\ &=& 2\left(\sum_{k=2}^\infty\left(P(k)-2^{-k}\right)\log k+\sum_{3\le p}\sum_{k=2}^\infty\frac{\log k}{p^k}\frac1{p-2}\right)\;. \end{eqnarray*}
The single sum in the first term is the one that occurred for even numbers adjacent to a single prime (see the link above); it evaluates to approximately $0.226201$. The terms of the double sum now decrease as $p^{-3}$, and it evaluates to approximately $0.163679$ (Wolfram|Alpha computation). The overall sum is thus approximately $0.779761$, so a large even number between twin primes is expected to have approximately $\mathrm e^{0.779761}\approx2.180950$ times as many divisors as usual, a substantially greater effect than for even numbers adjacent to a prime. (Note that this is the geometric mean, since we used the expected value of the logarithm; if you average the divisor counts themselves, you'll get a slightly higher result, since the geometric mean is less than the arithmetic mean.)
P.S.:
Here's some numerical evidence that these calculations are correct. The plot shows the excesses over the average for even numbers between twin primes, averaged up to $10^k$ with $k=3,\cdots,8$ ($k$ is marked on the $x$ axis). The additive excess in distinct prime factors is shown with red crosses; the red line shows the calculated limit. The logarithmic excess in divisors is shown with blue crosses; the blue line shows the calculated limit. The values are far from converged but are entirely compatible with the calculated limits. Here's the code I used to generate the data.
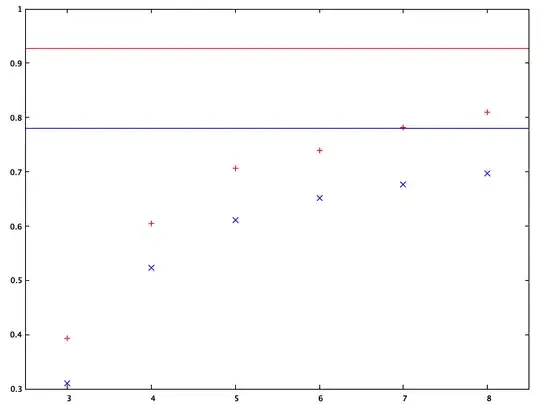
P.P.S.:
In this answer, Nilotpal Kanti Sinha provides numerical data for the excesses of numbers between twin primes over numbers on either side of twin primes. We can apply the present analysis also to the numbers on either side of twin primes. For $p\ge5$, the analysis remains the same, as two non-zero residues are excluded for each $p\ge5$. However, for $p=3$, the effect is reversed. Whereas a number between twin primes is always divisible by $3$ (which accounts for $\frac23$ of the $0.927$ excess distinct prime factors, since an arbitrary number only has probability $\frac13$ of being divisible by $3$), a number on either side of twin primes is never divisible by $3$. Since the contributions from $p\ge5$ are the same, the excess in distinct prime factors of numbers between twin primes over numbers on either side of twin primes is exactly $1$. (This can't be compared to Nilotpal Kanti Sinha's results, since they are expressed multiplicatively, and in the case of the number of distinct prime factors the multiplicative excess vanishes in the limit, since the additive excess converges and the expected number of distinct prime factors diverges.)
For the expected number of divisors, we likewise need to remove the term for $p=3$ from the sum. This is
$$ 2\sum_{k=1}^\infty\frac{\log(k+1)}{3^k}\approx0.871677\;. $$
This logarithmic excess leads to a multiplicative excess of approximately $\mathrm e^{0.871677}\approx2.390917$ in the number of divisors of numbers between twin primes over numbers on either side of twin primes, in rough agreement with Nilotpal Kanti Sinha's results. As can be seen from the diagram above, better agreement is not to be expected for data accessible to quick computer searches.
Yes there is something interesting about the composite number between twin primes. Let $p,p+2$ be a twin prime pair. Then $p-1$ is the composite number just preceding the pair, $p+1$ is the composite number between the pair and $p+3$ is the composite number just after the pair. Let $d(n)$ and $\omega(n)$ be the number of divisors and the number of distinct prime factors of $n$ respectively. Then, experimental data shows that
$$ 2.27 \sum_{p,p+2 \in P}{d(p-1)} \approx 2.27 \sum_{p,p+2 \in P}{d(p+3)} \approx \sum_{p,p+2 \in P}{d(p+1)} $$
$$ 1.24 \sum_{p,p+2 \in P}{\omega(p-1)} \approx 1.24 \sum_{p,p+2 \in P}{\omega(p+3)} \approx \sum_{p,p+2 \in P}{\omega(p+1)} $$
i.e. roughly speaking, the composite number between a twin prime pair has on an average $24\%$ more distinct prime factors than the composite number just before or just after the pair and more than twice as many divisors.
I shall post this in a separate question with the detailed data not only for twin prime but similar observations for other prime gaps.
Other than $n=4$, $n$ has the property that for every prime number $q=6k\pm 1$, $\frac{n}{6}\not \equiv \pm k \bmod q$.
Let $m:=\frac{n}{6};\ 6m=n$ and the twin primes $(n-1),(n+1)$ are represented as $(6m-1),(6m+1)$
We see from the properties of the semiprime $(6m-1)(6m+1)=36m^2-1$. If $36m^2-1$ is not a semiprime, it is divisible by some prime $6k\pm 1,\ k\ne m$. In other words $36m^2-1=(6k\pm 1)(6j\pm 1)$ where $k,j\ne m$. Expanding, $36m^2-1=36jk\pm 6j \pm 6k-1$ which reduces to $6m^2=6jk\pm j \pm k$
This means $m^2=jk \pm \frac{j\pm k}{6}$, and since $m^2$ is an integer, $\frac{j\pm k}{6}$ must be an integer, call it $r$. So $j=6r\pm k$ and we can substitute this back to obtain $m^2=(6r\pm k)k \pm r=k^2\pm r(6k\pm 1)$.
Finally we obtain $m^2-k^2=(m-k)(m+k)=r(6k\pm 1)$. This means that $(m-k)(m+k)\equiv 0 \bmod q$ which can only be true if $m\equiv \pm k \bmod q$.
So if $36m^2-1$ is not a semiprime, then $m\equiv \pm k \bmod q$ when $q\mid 36m^2-1$. But if $(6m-1),(6m+1)\in \mathbb P$ then $36m^2-1$ is a semiprime, so for every prime number $q=6k\pm 1$, $m\not \equiv \pm k \bmod q \Rightarrow \frac{n}{6}\not \equiv k \bmod q$.
$n-1,n+1$ are both primes iff for all prime $p\le \sqrt{n}, n \not \equiv \pm 1\bmod p$.
The random model for the primes, from which we predict the density of twin primes, is that those conditions are more or less independent from one $p$ to the other, ie. $n$ has nothing else special.
My conjecture is that there is a „local sieve“ around a twin prime pair such that all prime factors up to the square root of the higher prime are to find in the surrounding composite numbers in a maximum distance equal to the highest prime below this square root, relative to the number between the twin prime pair. If that is guaranteed, there are simply no prime factors left, and the pair must be prime. Since the number between the pair must be divisible by 6, it is always at least one to two primes ahead of its surrounding composites, and it is allowed to accumulate a lot more prime factors since neighboring integers cannot have common divisors, which also lets other composites in the surroundings accumulate prime factors. Does this, in average, give a Gaussian? - Of course, that‘s just an idea and a very coarse outline of a „local sieve“ for twin primes or primes in general.
