1

I am stuck on a problem that requires me to solve the half period length of a sine wave given a fixed "arc" length of the sine wave and variable maximum amplitude. I have illustrated the problem:

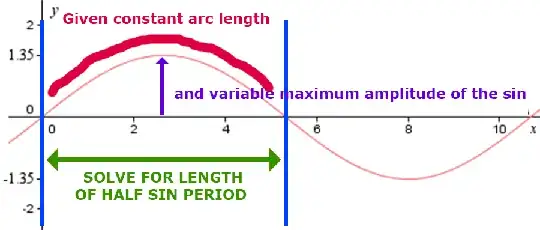
enter image description here

Is this problem solvable? Can it be approximated in any reasonably inexpensive computational way? It is for a problem where I will need to be constantly recalculating it based on the amplitude changes (say from 0 to 1).

Thanks.

Community
  • 1
mike
  • 381
  • What's the significance of the quotes around "arc"? Do you mean something other than what "arc length" refers to in standard usage? – joriki Dec 29 '19 at 07:31
  • Also, it's not clear to me what distinction you're making between the "fixed" arc length and the "variable" amplitude of the sine wave. If I understand correctly, both of these are given? – joriki Dec 29 '19 at 07:33
  • The fixed arc length does not change over time. The amplitude of the sine wave does change over time. Both are given. But only the amplitude of the sine wave changes. Then I want to know the half period length from that. The quotes are around the word arc because an arc is a portion of a circle. A sine wave is not an arc. It just looks like an arc so that's what I called it. – mike Dec 29 '19 at 09:27
  • It's not clear to me how the change over time is relevant to the problem. How is this problem different from if you just stated that the arc length and the amplitude are given and you're looking for the (half) period? Regarding the definitions of "arc" and "arc length", see https://www.dictionary.com/browse/arc?s=t ("any unbroken part of the circumference of a circle or other curved line") and https://en.wikipedia.org/wiki/Arc_length ("Arc length is the distance between two points along a section of a curve."). No quotes required. – joriki Dec 29 '19 at 12:02

1 Answers1

1

In general, the length of a sinusoid over a half period is a complete elliptic integral; see What is the length of a sine wave from $0$ to $2\pi$? You can work from an amplitude and a period to get an arc length, but "inverting" the calculation of the integral to get a period for a given amplitude and arc length will be difficult and probably computationally expensive.

What I would suggest instead is to generate a table that gives the periods for a fixed arc length and selected amplitudes, and interpolate within that table to get results for other amplitudes.

To generate entries in the table, you could fix the period -- say, $2\pi$ for convenience -- and find the arc length for various amplitudes. For the curve $y = a \sin x$ of amplitude $a$, the arc length is

$$ \newcommand{d}{\,\mathrm d} L(a) = \int_0^{2\pi} \sqrt{1 + a^2 \cos^2 x} \d x. $$

Now you can scale the entire figure in all directions by a factor of $1/L(a)$ to obtain the curve $$y = \frac{a}{L(a)} \sin(L(a)\cdot x)$$ which has amplitude $\frac{a}{L(a)}$, half-period $\frac{\pi}{L(a)},$ and arc length $1.$ Put that amplitude and half-period in your table.

To get the half-period for a given arc length $L$ and amplitude $A,$ look up the value $\frac AL$ in the "amplitude" column of your table, find the interpolated half-period using the table, and then multiply the interpolated value by $L.$

Generating the table requires some work in advance but you can do that work once and store the results in a data file that can be read in at the start of your program and used over and over. The more values you calculate in advance, the more accurate the interpolation will be; you can also use cubic splines instead of linear interpolation to get more accuracy with the same number of rows in your table.

David K
  • 108,155