EDIT: Now a full solution is given for $n \le 10^9$ (if this limitation is an issue at all, discussion and possible extension see below).
Due to homogenity, the task is equivalent to the following: Find the maximum of the target function
$$
f(x) = \left(\sum_{k=1}^{n}x_{k}\cos{k}\right)^2+\left(\sum_{k=1}^{n}x_{k}\sin{k}\right)^2
$$
subject to $\sum_{k=1}^{n}x_{k}^2 = {\rm{const.}}$, and then show that this maximum is less or equal than $\left(2+\dfrac{n}{4}\right)\cdot{\rm{const.}}$. In order to see which $x_k$ will generate this maximum, let's derive a necessary condition: At the maximum, consider changing two $x_k$'s, say $x_n$ and $x_m$, while keeping all other $x_k$ fixed. Then, for small changes $\delta x_n$, $\delta x_m$, since $\sum_{k=1}^{n}x_{k}^2 = {\rm{const.}}$, the condition is
$x_n \delta x_n = - x_m \delta x_m$. The change in the target function is
$$
\delta f(x) = 2 \left(\sum_{k=1}^{n}x_{k}\cos{k}\right)(\cos(n) \delta x_n + \cos(m) \delta x_m) +2 \left(\sum_{k=1}^{n}x_{k}\sin{k}\right)(\sin(n) \delta x_n + \sin(m) \delta x_m)\\
= \left[ 2 \left(\sum_{k=1}^{n}x_{k}\cos{k}\right)(\cos(n) - \cos(m) \frac{x_n}{x_m}) +2 \left(\sum_{k=1}^{n}x_{k}\sin{k}\right)(\sin(n) - \sin(m) \frac{x_n}{x_m}) \right] \delta x_n
$$
Since $\delta f(x)$ must be zero at the optimum, we have the condition that
$$
\frac{x_n}{x_m} = \frac{
\cos(n) + a\sin(n)
}{
\cos(m) + a\sin(m)
} \qquad , {\rm{with }} \qquad a = \frac{
\sum_{k=1}^{n}x_{k}\sin{k}}{\sum_{k=1}^{n}x_{k}\cos k}
$$
Since this must hold for all pairs $(x_n, x_m)$, and since $x_k \ge 0$, the optimum is reached at
$x_k = \tilde c \cdot \max\{0, \cos(k) + a \sin(k)\}$, with an arbitrary constant $\tilde c$, for all $x_k$, with $a$ to be fixed through the implicit equation $$a = \frac{
\sum_{k=1}^{n}x_{k}\sin{k}}{\sum_{k=1}^{n}x_{k}\cos k} $$
However this is inconclusive for $a$, see appendix A below. Hence we shall prove that such $x_k$ satisfy the inequality, for any $a$. The form of $x_k$ can equivalently be written $x_k =c \cdot \max\{0, \sin(k + \phi)\}$, with an arbitrary constant $c$, and some angle $\phi$.
Note that the LHS of the inequality is, for any $x_k$, $\left(\sum_{k=1}^{n}x_{k}\cos{k}\right)^2+\left(\sum_{k=1}^{n}x_{k}\sin{k}\right)^2 = \left(\sum_{k=1}^{n}x_{k}\cos{(k+\gamma)}\right)^2+\left(\sum_{k=1}^{n}x_{k}\sin{(k+\gamma)}\right)^2$ with some arbitrary $\gamma$, which holds since $$\left(\sum_{k=1}^{n}x_{k}\cos{k}\right)^2+\left(\sum_{k=1}^{n}x_{k}\sin{k}\right)^2 \\= \sum_{k=1}^{n} \sum_{m=1}^{n} x_k x_m
\cos(k-m) = \sum_{k=1}^{n} \sum_{m=1}^{n} x_k x_m
\cos((k+\gamma)-(m+\gamma)) $$
Using this freedom, let us choose $\gamma = \phi$. Now we will estimate the two terms of the inequalty's LHS separately.
Second term: We have that
$$
\left(\sum_{k=1}^{n}x_{k}\sin{(k+\phi)}\right)^2 \le \left(\sum_{k=1}^{n}x_{k}\max\{0, \sin(k + \phi)\}\right)^2
$$
Applied to the square we have
$(\sum_{k=1}^{n}x_{k}\sin{(k + \phi)})^2 \le (\sum_{k=1}^{n}x_{k}\max\{0,\sin{(k + \phi)} \})^2$
and
$(\sum_{k=1}^{n}x_{k}\sin{(k + \phi)})^2 = (-\sum_{k=1}^{n}x_{k}\sin{(k + \phi)})^2 \le (\sum_{k=1}^{n}x_{k}\min\{0,\sin{(k + \phi)} \})^2 $.
Either one of these inequalities is used, depending on whether $\sum_{k=1}^{n}x_{k}\sin{(k + \phi)} >0 $ or $<0$.
Applying Cauchy-Schwarz gives
$$
\frac{ (\sum_{k=1}^{n}x_{k}\sin{(k + \phi)})^2}{\sum_{k=1}^{n}x_{k}^2} \le \sum_{k=1}^{n} (\max\{0,\sin{(k + \phi)} \})^2 \\
= \frac12 \sum_{k=1}^{n} (\sin{(k + \phi)} )^2 + \frac12 \sum_{k=1}^{n} |\sin{(k + \phi)}| \sin{(k + \phi)}
$$
or
$$
\frac{ (\sum_{k=1}^{n}x_{k}\sin{(k + \phi)})^2}{\sum_{k=1}^{n}x_{k}^2} \le \sum_{k=1}^{n} (\min\{0,\sin{(k + \phi)} \})^2 \\
= \frac12 \sum_{k=1}^{n} (\sin{(k + \phi)})^2 - \frac12 \sum_{k=1}^{n} |\sin{(k + \phi)}| \sin{(k + \phi)}
$$
It has been shown in this post that, for any $\phi$, the second sum is $\le 1.75$. Further we have
$$
|\sum_{k=1}^{n} (\sin{(k + \phi)})^2 |= |\frac{n}{2} + \frac{\sin(2\phi + 2 n + 1) )-\sin(2 \phi + 1) )}{4 (\sin(1))}| \le \frac{n}{2} + \frac{1}{2 (\sin(1))}
$$
Combing the two limits we get for the second term:
$$\frac{ (\sum_{k=1}^{n}x_{k}\sin{(k + \phi)})^2}{\sum_{k=1}^{n}x_{k}^2} \le
\frac{n}{4}+ 1.17$$
Note that the only condition used for the $x_k$ was their positivity.
First term: Now we use the particular form of the $x_k$. We have for the sum within the square, using the heaviside-function $\Theta(x)$:
$$
\sum_{k=1}^{n}x_{k}\cos{(k+\phi)} \le c \sum_{k=1}^{n}\cos{(k+\phi)}\max\{0, \sin(k + \phi)\} \\
= \frac{c}{2} \sum_{k=1}^{n}\sin{(2k+2\phi)}\Theta\{\sin(k + \phi)\}\\
= \frac{c}{4} \left[\sum_{k=1}^{n}\sin{(2k+2\phi)}
+ \sum_{k=1}^{n}(\sin{(2k+2\phi)}\Theta\{\sin(k + \phi)\}- \sin{(2k+2\phi)}\Theta\{-\sin(k + \phi)\})\right]
$$
For the first sum, we have
$$
|\sum_{k=1}^{n}\sin{(2k+2\phi)}|= |\frac{\sin(n) \sin(2 \phi + n + 1)}{\sin(1)}| \le \frac{1}{\sin(1)} \le 1.19
$$
The second sum can be evaluated to be less than $\alpha = 2.4 +\frac{1}{2 \pi} (3\log(M + 1/2)) + \log(M - 3/2)) + \frac{8n}{\pi} \frac{M}{4M^2-1} $ for some $M \le 10^9$ (see appendix B). Combining the two, we have
$$
|\sum_{k=1}^{n}x_{k}\cos{(k+\phi)}| \le
\frac{c}{4} \left[1.17 + \alpha\right]
$$
Further, we have analogously to the derivation above:
$$
|\sum_{k=1}^{n}x_{k}^2 |= c^2|\sum_{k=1}^{n}(\max\{0,\sin{(k + \phi)} \})^2 |\ge c^2(\frac{n}{4}- 1.17)$$
This gives for the first term of the inequality's LHS, normalized to the length of $x$:
$$
\frac{(\sum_{k=1}^{n}x_{k}\cos{(k+\phi)})^2}{\sum_{k=1}^{n}x_{k}^2} \\
\le
\frac{(\frac{1}{4} \left[3.57 +\frac{1}{2 \pi} (3\log(M + 1/2)) + \log(M - 3/2)) + \frac{8n}{\pi} \frac{M}{4M^2-1} \right])^2}{\frac{n}{4}- 1.17}
\le
\frac{(\frac{1}{4} \left[3.57 +\frac{2}{ \pi} \log(M + 1/2) + \frac{8n}{\pi} \frac{1}{3M} \right])^2}{\frac{n}{4}- 1.17}
$$
We have the freedom of choosing $M \le 10^9$, which we can use to minimize this expression. The minimum occurs at $M = 1/3 (\sqrt(2) \sqrt{(2 n^2 + 3 n)} + 2 n)$ so we choose $M = \frac{4 n }{3}$ which gives
$$
\frac{(\sum_{k=1}^{n}x_{k}\cos{(k+\phi)})^2}{\sum_{k=1}^{n}x_{k}^2} \\
\le
\frac{(\frac{1}{4} \left[3.57 +\frac{2}{ \pi} \log(\frac{4 n }{3} + 1/2) + \frac{2}{\pi} \right])^2}{\frac{n}{4}- 1.17}
\\
\le
\frac{(\frac{1}{4} \left[\frac{2\log(n)}{ \pi} + \frac{2}{ \pi} \log(\frac{4 }{3} ) + \frac{2}{\pi} + 3.57 \right])^2}{\frac{n}{4}- 1.17}
\\
\le
\frac{(\frac{1}{4} \left[\frac{2\log(n)}{ \pi} + 4.4\right])^2}{\frac{n}{4}- 1.17} = \frac{\left[\frac{\log(n)}{ 8 \pi} + 0.275\right]^2}{\frac{n}{4}- 1.17}
$$
This result makes sense for reasonably large $n\ge 5$, which is an artefact of having to apply a lower bound for the denominator. This can be traeted if necessary. The result is strictly falling with $n$, so we can bound it for $n\ge 5$by the result for $n = 6$ which is 0.36. This is a very rough bound, since for large $n$ this gets considerably smaller, already for $n=20$ we have 0.04. Note the result holds for $n \le 10^9$, if this is considered a limitation, it can be expanded (see appendix B).
Combining the two terms finally gives for the inequality:
$$\left(\sum_{k=1}^{n}x_{k}\cos{k}\right)^2+\left(\sum_{k=1}^{n}x_{k}\sin{k}\right)^2 \le (\frac{n}{4}+ 1.54 )\sum_{k=1}^{n}x_{k}^2
$$
Appendix A:
Calculating the implicit equation for $a$ gives inconclusive results, as will be shown here:
$$a = \frac{
\sum_{k=1}^{n}x_{k}\sin{k}}{\sum_{k=1}^{n}x_{k}\cos k} =
\frac{
\sum_{k ; \cos(k) + a \sin(k) > 0} (\cos(k) + a \sin(k))\sin{k}
}
{
\sum_{k ; \cos(k) + a \sin(k) > 0} (\cos(k) + a \sin(k))\cos k
} \\
= \frac{
\sum_{k ; \cos(k) + a \sin(k) > 0} \cos(k) \sin{k} + a \sum_{k ; \cos(k) + a \sin(k) > 0} \sin^2(k)
}
{
\sum_{k ; \cos(k) + a \sin(k) > 0} \cos(k) \sin{k} + a \sum_{k ; \cos(k) + a \sin(k) > 0} \cos^2(k)
}\\
= \frac{
2\sum_{k ; \cos(k) + a \sin(k) > 0} \cos(k) \sin(k) + a \sum_{k ; \cos(k) + a \sin(k) > 0} 1 {\color{red}+} a \sum_{k ; \cos(k) + a \sin(k) > 0}(\sin^2(k) - \cos^2(k))
}
{
2\sum_{k ; \cos(k) + a \sin(k) > 0} \cos(k) \sin(k) + a \sum_{k ; \cos(k) + a \sin(k) > 0} 1 {\color{red}-} a \sum_{k ; \cos(k) + a \sin(k) > 0}(\sin^2(k) - \cos^2(k))
}\\
= \frac{
\sum_{k ; \cos(k) + a \sin(k) > 0} \sin(2 k)+ a \sum_{k ; \cos(k) + a \sin(k) > 0} 1 {\color{red}-} a \sum_{k ; \cos(k) + a \sin(k) > 0} \cos(2 k)
}
{
\sum_{k ; \cos(k) + a \sin(k) > 0} \sin(2 k) + a \sum_{k ; \cos(k) + a \sin(k) > 0} 1 {\color{red}+} a \sum_{k ; \cos(k) + a \sin(k) > 0}\cos(2 k)
}$$
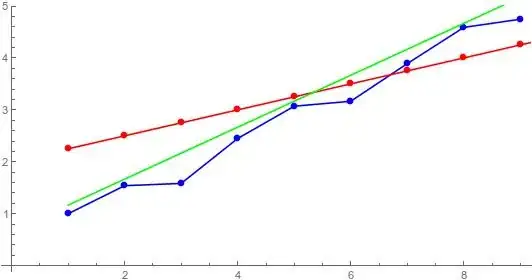
Since, for large $n$, $\sum_{k ; \cos(k) + \sin(k) > 0}\cos(2 k)$ is of the same order as $\sum_{k ; \cos(k) + \sin(k) > 0} 1 $, this gives no clear indication of $a$. The inituitive $a\simeq 1$ does not hold, as the following example shows, which was generated through computer search to find, for varying $n$ and $a$, the highest value of $$\frac{\left(\sum_{k=1}^{n}x_{k}\cos{k}\right)^2+\left(\sum_{k=1}^{n}x_{k}\sin{k}\right)^2}{\sum_{k=1}^{n}x^2_{k}} - \frac{n}{4}$$ The result is:
Let $a = 6.47$ and $n=10256$, then setting $x_k = \max\{0, \cos(k) + a \sin(k)\}$ gives
$$
\left(\sum_{k=1}^{n}x_{k}\cos{k}\right)^2+\left(\sum_{k=1}^{n}x_{k}\sin{k}\right)^2\le \left({\color{red}{1.0466}}+\dfrac{n}{4}\right)\sum_{k=1}^{n}x^2_{k}
$$
Since $n$ is large, this shows the leading proportionality to $n/4$.
Appendix B: For the sum
$$
S_n = \sum_{k=1}^{n}(\sin{(2k+2\phi)}\Theta\{\sin(k + \phi)\}- \sin{(2k+2\phi)}\Theta\{-\sin(k + \phi)\})
$$
we use the following Fourier series representation:
$$
\sin{(2x)}\Theta\{\sin(x)\}- \sin{(2x)}\Theta\{-\sin(x)\}\\
= \frac{1}{\pi}\sum_{m=0}^{\infty} \frac{-8}{(2m+1)^2 - 4} \cos((2m+1)x)
$$
This allows us to write
$$
S_n = \frac{1}{\pi}\sum_{m=0}^{\infty} \frac{-8}{(2m+1)^2 - 4} \sum_{k=1}^{n}\cos((2m+1)(k+\phi))\\
= \frac{1}{\pi}\sum_{m=0}^{\infty} \frac{-8}{(2m+1)^2 - 4} \frac{\sin((m + 1/2) n) \cos(1/2 (2 m + 1) (n + 2 \phi + 1))}{\sin(m + 1/2) }
$$
Now we have the following fact which can be evaluated by computer: we have that
$\frac{1}{|\sin(m + \frac12)|}<m$ for almost all $m \in [2,10^9]$, other than very few exceptions, i.e. $m_R \in \{9,12,166,188, 51996, 156344,990063,2136471,40071928,205778993\}$.
Note 1: if this limitation(which we will also apply to $n$) is an issue at all, it can be verified by computer for higher terms as well, with few exceptions which do not hamper the overall result.
Note 2: The bound can be further tightened, see Jack D'Aurizio's answer in this post which discusses $\frac{1}{\left|\sin m\right|}\leq \frac{\pi/2}{d(m,\pi\mathbb{Z})}$.
This allows to write, with $M \le 10^9$:
$$
S_n = \frac{1}{\pi}[\sum_{m=0}^{1} +\sum_{m=2}^{M-1} + \sum_{m=M}^\infty] \frac{-8}{(2m+1)^2 - 4}\frac{\sin((m + 1/2) n) \cos(1/2 (2 m + 1) (n + 2 \phi + 1))}{\sin(m + 1/2) }
$$
The first two terms evaluate
$$
|S_n^{(1)}| \le \frac{1}{\pi} (\frac{8}{3 |\sin(\frac12)|} + \frac{8}{5 |\sin(\frac32)|} ) \le 2.28
$$
For the second part, we bound
$$
|S_n^{(2)}| = \frac{1}{\pi} \sum_{m=2}^{M-1} | \frac{8}{(2m+1)^2 - 4} \frac{1}{ \sin(m + \frac12)}|
\\
\le \frac{8}{\pi} \sum_{m=2}^{M-1} | \frac{m}{(2m+1)^2 - 4} | + \frac{8}{\pi} \sum_{m_R} |\frac{8}{(2m+1)^2 - 4}(\frac{1}{ \sin(m_R + \frac12)} -m_R)| \\
\le \frac{8}{\pi} \int_{m=2}^{M-1} | \frac{m}{(2m+1)^2 - 4} | + \frac{8}{\pi} \sum_{m_R} |\frac{8}{(2m+1)^2 - 4}(\frac{1}{ \sin(m_R + \frac12)} -m_R)| \\
\le \frac{1}{2 \pi} (3\log(M + 1/2)) + \log(M - 3/2)) + \frac{8}{\pi} \sum_{m_R} |\frac{8}{(2m+1)^2 - 4}(\frac{1}{ \sin(m_R + \frac12)} -m_R)| \
$$
The third part can be bounded, using that $\frac{\sin(n(m + \frac12)) }{ \sin(m + \frac12)} \le n$, with
$$
|S_n^{(3)}| = \frac{8 n }{\pi} \sum_{m=M}^{\infty} \frac{1}{(2m+1)^2 - 4}
\\
\le \frac{8n}{\pi} |\frac{M}{4M^2-1} |
$$
and altogether
$$
|S_n| \le 2.4 +\frac{1}{2 \pi} (3\log(M + 1/2)) + \log(M - 3/2)) + \frac{8n}{\pi} \frac{M}{4M^2-1}
$$