0

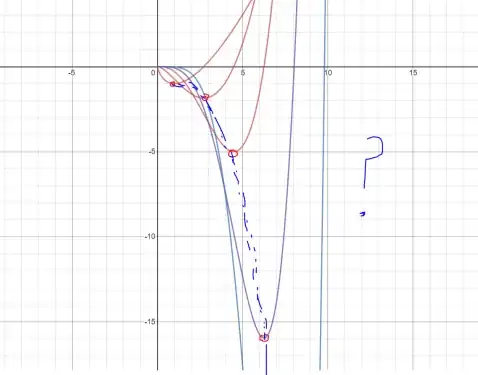
Graph of repeated integrals of ln(x)

It's just something I noticed while graphing the repeated integrals (C = 0) of ln (x). I'm not exactly sure how to prove that they do trace out a logarithmic curve. I did find this post on math stackexchange which is able to find the nth integral of 1/x (or the (n-1)th integral of ln (x)), and I was thinking of using that to find the zeroes of the previous integral (which is the turning points of the next one): What's the nth integral of $\frac1{x}$? Also see: Does the repeated integral of $\ln x$ have a pattern?

I hope you find it an interesting problem as I did, and maybe we can come up with something here.

James Turbett
  • 107
  • 6

1 Answers1

1

Following your link, we obtain a formula for the nth integral of 1/x, so we can study what happens as n goes to infinity. We have that $lim_(n->∞)$$x^(n-1)/((n - 1)!)=0$ since generally n! is larger than a^n (Do factorials really grow faster than exponential functions?).

So this means that we are left with a linear combination of x, so we have $c_1$x+$c_1$x+.......=Ax where A is an infinite sum. It really depends on what this A is. If A=0 for example then we have y=0, the real axis. (Graphs of first few integrals of 1/x https://www.desmos.com/calculator/cqowlr8b9p). You can see it from your sketch that the graphs are stretching out form the origin, so if C=0, you get the positive real line.

Alessio K
  • 10,679