Using calculus to find the winding number of $\sin(2t)+i\cos(t)$

Question

To calculate an integral I need to find the winding number of $$\gamma(t)=\sin(2t)+i\cos(t)$$ around $\frac{i}{2}$. Graphically it looks like it is $1$. How can I use calculus to show this rigorously? I don't know how to calculate $$\int_{-\pi/2}^{3\pi/2}\frac{2\cos(2t)-i\sin(t)}{\sin(2t)+i\cos(t)-\frac{i}{2}}dt$$Do I even have to? (Directly)

Answer 1

It suffices to define a consistent arg function for $\ln(\gamma(t)-\frac i 2)$ on $[\frac \pi 2,\frac{3\pi}2]$. I suggest the following: $$f(t)=\left\{\begin{array}{cc}-\frac \pi 2,&t =\frac \pi 2,\pi,\frac{3\pi}2\\ \tan^{-1}\left(\frac {2\cos(t)-1}{2\sin(2t)}\right)-\pi,&\frac \pi 2<t<\pi\\ \tan^{-1}\left(\frac{2\cos(t)-1}{2\sin(2t)}\right),&\pi<t<\frac{3\pi}2\end{array}\right.$$ This is well defined and continuous, so the winding number is zero.

[Edit] More details: paraphrasing Wikipedia, if $\gamma$ is a closed curve parameterized by $t\in [\alpha,\beta],$ the winding number of $\gamma$ about $z$ is $${\rm Ind}_{\gamma}(z)=\frac 1{2\pi i}\int_{\alpha}^{\beta}\frac{\gamma'(t)}{\gamma(t)-z}~dt .$$ In the special case here $z=\frac i2$ and we are considering the behavior about how the curve $\gamma(t)$ is winding around $\frac i 2$. The argument (angle) of $\gamma(t)$ with respect to $\frac i 2$ can be seen from the complex number $$\gamma(t)-\frac i 2=\sin(2t)+\frac{2\cos(t)-1}2i.$$ Taking hint from polar coordinates, the angle of this complex number is related to $$\tan^{-1}\left(\frac {2\cos(t)-1}{2\sin(2t)}\right).$$ As in the definition of $f(t)$, this angle is wavering between the values $$-\frac \pi 2\sim \delta-\pi\sim- \frac \pi 2\sim -\delta\sim -\frac \pi 2,$$ where $\frac \pi 2>\delta>0$ and $-\delta$ is the maximum of $f$ on $[\frac \pi 2,\frac{3\pi}2]$. Note that here the arctan takes values in $(-\frac\pi 2,\frac \pi 2), $but the function $f$ takes values in $[\delta-\pi,-\delta]$, a subinterval of $(-\pi,0)$. Nevertheless $f(\frac\pi 2)=f(\frac{3\pi}2)=-\frac\pi 2$, so the total change of angle equals zero.

Answer 2

It looks as if you mean $\gamma$ to be defined on the interval $[0, 2\pi]$, although the limits of the integral expression give a different and misleading impression - and as the other answer correctly states, the winding number is zero if the parameter interval is $[\pi/2, 3\pi/2]$.

Let $\gamma_1$, $\gamma_2$, $\gamma_3$ be the restrictions of $\gamma$ to the intervals $[0, \pi/2]$, $[\pi/2, 3\pi/2]$, $[3\pi/2, 2\pi]$, respectively.

I'm afraid this hastily-produced figure lacks a caption, and the point with parameter value $3\pi/2$ has overwritten the point with parameter value $\pi/2$, because both are at the origin:

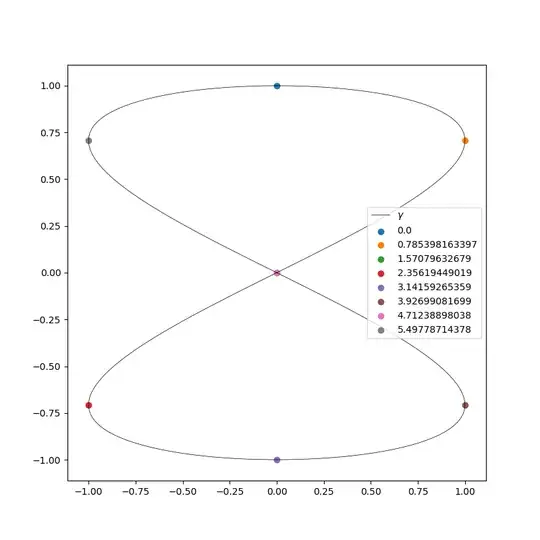
$\gamma_2$ is a closed curve, contained in the open half-plane $\{z : \Im z < 1/2\}$, on which there is a continuous choice of argument for $z - i/2$, for example one with values in $(-3\pi/2, \pi/2)$, so the winding number of $\gamma_2$ about $i/2$ is $0$.

Each of $\gamma_1$, $\gamma_3$ separately also has a continuous choice of argument for $z - i/2$, although their concatenation, the closed curve $\gamma_1 + \gamma_3$, does not.

(Correction: that was very badly put! Every curve has a continuous choice of $\arg(z - w)$, for any point $w$ not on the curve; and indeed the very concept of winding number I'm appealing to here depends on that proposition. I should have said something to the effect that the construction of such a function for $\gamma_1 + \gamma_3$ has to be done piecewise, most naturally for $\gamma_1$ and $\gamma_3$ separately; and this is because $\gamma_1 + \gamma_3$ isn't contained in any domain on which there is a continuous choice of argument for $z - i/2$. I hope this hasty correction will suffice.)

For instance, the principal value of $\arg(z - i/2)$ could be used for $\gamma_1$, and the winding number of $\gamma_1$ about $i/2$ is then computed as: $$ \frac{\arg(0 - i/2) - \arg(i - i/2)}{2\pi} = \frac{-\pi/2 - \pi/2}{2\pi} = -\frac12. $$

For $\gamma_3$, you could choose a continuous argument function, call it $\arg_3$, whose value varies in the range $(0, 2\pi)$ (undefined on the non-negative real axis), and the winding number of $\gamma_3$ about $i/2$ is then computed as: $$ \frac{\arg_3(i - i/2) - \arg_3(0 - i/2)}{2\pi} = \frac{\pi/2 - 3\pi/2}{2\pi} = -\frac12. $$

The winding number of $\gamma$ about $i/2$ is the sum of the winding numbers of $\gamma_1$, $\gamma_2$, $\gamma_3$ about $i/2$, which evaluates to: $$ -\frac12 + 0 - \frac12 = -1. $$