I have a grid 5x5 and I have to fill 16 little squares with a diagonal
Rules
Click here to view the solution
But what I seek here is a mathematical solution for this puzzle, I don't even know where to start looking for information.
Can someone explain how do I solve this puzzle using equations?
Think of it this way: You have a 5x5 array, and you need to fill it with values 0, 1, or -1, with three restrictions:
Here, cells containing a "1" have a diagonal running top-left to bottom-right, and cells containing a "-1" have a diagonal running the other way. Cells containing 0 do not have a diagonal at all.
So, for the example grid you provide, you start with the grid:
$$ \begin{matrix}0&0&-1&0&0\\0&-1&0&-1&1\\0&0&0&0&0\\0&0&0&0&0\\0&0&0&0&0\end{matrix} $$
I don't think there's "a mathematical solution" to it - that is, I doubt that one could immediately find the "right answer" without some level of trial and error. But it does give a good starting point to automating the search, if you want to try solving it computationally.
I have written a brute force search, which seems to work. But it would take days to inspect the $3^{25} = 847,288,609,443$ configurations or reimplementation of some parts in C.
Some feasible solutions from a random walk:
[ 45.33%] [1100201102001021010210022] found: len = 14 [max = 14]
/ / . . \
. / / . \
. . / . \
/ . / . \
/ . . \ \
[ 41.74%] [1020210202102021101001001] found: len = 14 [max = 14]
/ . \ . \
/ . \ . \
/ . \ . \
/ / . / .
. / . . /
[ 99.59%] [2222200000102011000011111] found: len = 14 [max = 14]
\ \ \ \ \
. . . . .
/ . \ . /
/ . . . .
/ / / / /
[ 38.82%] [1011110001111010000011111] found: len = 15 [max = 15]
/ . / / /
/ . . . /
/ / / . /
. . . . .
/ / / / /
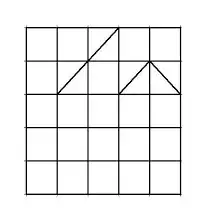
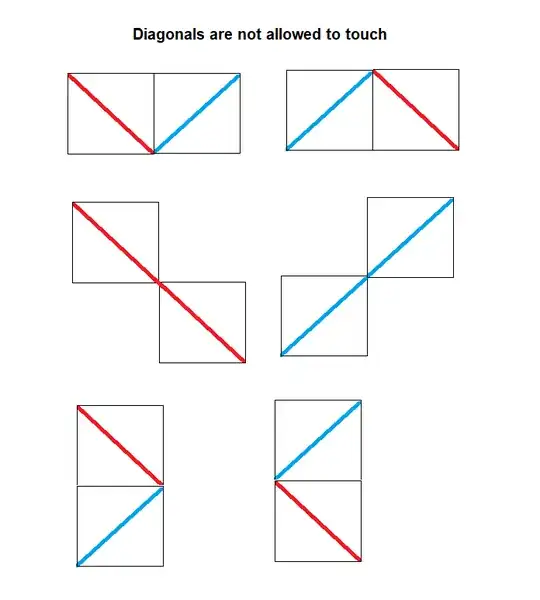
Between two adjacent rows of squares is a row of six corners. Each diagonal uses up one of them, so at most six diagonals in two adjacent rows.
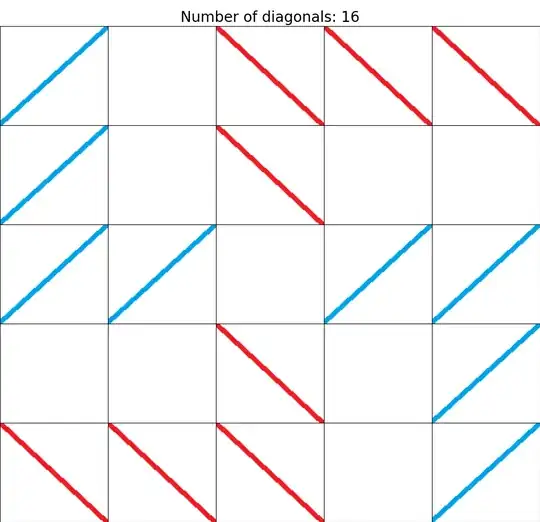
At most six diagonals in rows 1-2, six in rows 3-4, so at least four in row 5 to make sixteen. In the same way, rows 3 and 1 have at least four diagonals.
So rows 2 and 4 have at most two diagonals, or else you get more than six in two adjacent rows.
Seventeen is impossible: Since Row1+Row2 has at most six diagonals, and so does Row3+Row4, you need five diagonals in Row5. For the same reason, you need five in Row3 and Row1. But then you need one in either Row2 or Row4, and the only free corners do not allow a diagonal to join them.
Row3 can't have five diagonals: If it did, Row2 and Row4 could have only one each. That makes seven, leaving nine more between Row1 and Row5. So Row1 or Row5 has five as well. But, just as for the 'seventeen' case, if Row1 and Row3 both have five then Row2 must be empty; so Row4 and Row5 have six between them to make sixteen; So Row5 has five diagonals; so Row4 is empty; and we only have fifteen diagonals.
So Row3 has at most 4. Row1 and Row2 have at most six between them, and so do Row4 and Row5. So to make sixteen total, Row1 and Row2 have exactly six between them, as do Row4 and Row5. There are no spare corners between Row1 and Row2, nor between Row4 and Row5. So, once Row1 is chosen, there are at most four choices for Row2; and similar for Row5 and Row4.
There are 18 possible Row1s with at least four diagonals. There are 16 possible Row3s with exactly four diagonals.
Take the 18 possible Row1s, pair each with its possible Row2 to get a few dozen Row1Row2 pairs. For each pair, check which of the sixteen possible Row3s fits with the particular Row2. Having gone through all Row1Row2 pairs, you have a subset of the sixteen which can be part of a Row1RowRow3 triple.
To check whether that Row3 can attach to a Row4 and Row5, you just have to mirror-reflect it so that rising diagonals become falling diagonals, and check whether that reflection can be part of a Row1Row2Row3 triple.
This is a few hundred comparisons, that might take ten minutes by hand.
The solutions are (computer generated, main diagonal encoded as +1): cost = 16 $$ \begin{matrix}1&0&-1&-1&-1\\1&0&-1&0&0\\1&1&0&1&1\\0&0&-1&0&1\\-1&-1&-1&0&1\end{matrix} $$ and $$ \begin{matrix}1&1&1&0&-1\\0&0&1&0&-1\\-1&-1&0&-1&-1\\-1&0&1&0&0\\-1&0&1&1&1\end{matrix} $$ See also A264041 (solutions cost), A264667 (number of solutions)
If we encode the solution grid ($5 \times 5$) as a vector (of length $25$) and denote the diagonals / as 1 and \ as -1, e.g., with blank space in a cell as 0, we can use backtracking to solve the 16-diagonals problem.
Starting from empty solution vector the solution can be recursively extended with backtracking, at each stage checking if the partial solution is valid (i.e., none of the diagonals touch) with the function can_be_extended_to_solution() as shown in the next code snippet, otherwise discard the current solution.
The following figure shows what the function can_be_extended_to_solution() should check to ensure that there are no touching diagonals in the solution.
The function num_diag() counts the number of diagonals present in the solution so far, we can terminate if we have $16$ diagonals.
def can_be_extended_to_solution(solution_vector):
# check if any of the diagonals touch in the solution sol far
if ∃ a pair of touching diagonals in the solution:
return False
return True
def extend_solution_with_backtracking(solution_vector, n):
if len(solution_vector) == 25 and num_diag(solution_vector) == 16:
# found solution!
print(solution_vector)
exit()
for k in range(-1,2):
# try /, \ or blank in the next position
solution_vector.append(k)
if can_be_extended_to_solution(solution_vector):
extend_solution_with_backtracking(grid_vec, n)
solution_vector.pop()
def num_diag(solution_vector):
# return number of / or \ diagonals present in the solution
return sum([1 for x in solution_vectorif x != 0])
The following figure shows a solution obtained with the above backtracking algorithm.
The following animation shows how the partial solutions can be extended using backtracking:
