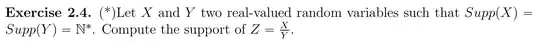In my lecture note, a real-valued random variable is defined as follows:
Then I have an exercise:
Actually, my lecture notes do not have a definition of a random variable generated by other ones.
We already have funtions $X : \Omega \to \mathbb{R}$ and $Y : \Omega \to \mathbb{R}$.
My question: What is the random variable $Z: \Omega \to \mathbb{R}$ by the symbol $Z= X/Y$? I mean, for each $\omega \in \Omega$, what is $Z(\omega)$?
Thank you so much for your help!