81

Given a matrix, is the Frobenius norm of that matrix always equal to the 2-norm of it, or are there certain matrices where these two norm methods would produce different results?

If they are identical, then I suppose the only difference between them is the method of calculation, eh?

Rodrigo de Azevedo
  • 23,223
Ricket
  • 1,181
  • 3
    What do you mean by 2-norm? – Jonas Meyer Apr 15 '11 at 01:59
  • 4
    The p-norm where p=2, also known as the Euclidean norm. – Ricket Apr 15 '11 at 02:02
  • 1
    If you mean the Euclidean norm when $M_n$ is treated like $\mathbb{C}^{n^2}$, then yes they are the same; this is the definition of the Frobenius norm, as seen on Wikipedia: http://en.wikipedia.org/wiki/Matrix_norm#Frobenius_norm – Jonas Meyer Apr 15 '11 at 02:06
  • 3
    Ricket: Could you please give the precise definitions you are using (or precise references to these definitions)? The phrase "p-norm" for matrices is ambiguous, which is why I asked earlier. Many think of "2-norm" as meaning the operator norm when $M_n$ acts on $\mathbb{C}^n$ with Euclidean norm, hence Yuval's answer. I think I now know what you mean, but then your question is answered by the Wikipedia link, right? – Jonas Meyer Apr 15 '11 at 02:26

4 Answers4

71

There are three important types of matrix norms. For some matrix $A$

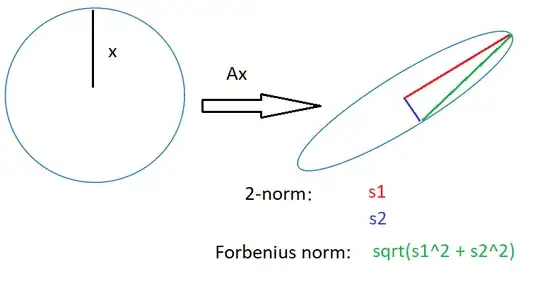
  • Induced norm, which measures what is the maximum of $\frac{\|Ax\|}{\|x\|}$ for any $x \neq 0$ (or, equivalently, the maximum of $\|Ax\|$ for $\|x\|=1$).

  • Element-wise norm, which is like unwrapping $A$ into a long vector, then calculating its vector norm.

  • Schatten norm, which measures the vector norm of the singular values of $A$.

So, to answer your question:

  • Frobenius norm = Element-wise 2-norm = Schatten 2-norm

  • Induced 2-norm = Schatten $\infty$-norm. This is also called Spectral norm.

So if by "2-norm" you mean element-wise or Schatten norm, then they are identical to Frobenius norm. If you mean induced 2-norm, you get spectral 2-norm, which is $\le$ Frobenius norm. (It should be less than or equal to)

As far as I can tell, if you don't clarify which type you're talking about, induced norm is usually implied. For example, in matlab, norm(A,2) gives you induced 2-norm, which they simply call the 2-norm. So in that sense, the answer to your question is that the (induced) matrix 2-norm is $\le$ than Frobenius norm, and the two are only equal when all of the matrix's eigenvalues have equal magnitude.

Brandon J. DeHart
  • 103
  • 5
Kevin Holt
  • 2,694
  • Great answer, but the last sentence is wrong. They are equal if all but one eigenvalue/singular value are zero. If $N$ singular values are equal (and the rest, if any, zero), then the Frobenius norm is $\sqrt N$ times the induced 2-norm – Daniel Dec 23 '23 at 23:53
53

The 2-norm (spectral norm) of a matrix is the greatest distortion of the unit circle/sphere/hyper-sphere. It corresponds to the largest singular value (or |eigenvalue| if the matrix is symmetric/hermitian).

The Forbenius norm is the "diagonal" between all the singular values.

i.e. $$||A||_2 = s_1 \;\;,\;\;||A||_F = \sqrt{s_1^2 +s_2^2 + ... + s_r^2}$$

(r being the rank of A).

Here's a 2D version of it: $x$ is any vector on the unit circle. $Ax$ is the deformation of all those vectors. The length of the red line is the 2-norm (biggest singular value). And the length of the green line is the Forbenius norm (diagonal). enter image description here

Maverick Meerkat
  • 1,410
  • 23
    I'm a simple man. When I see a geometric explanation, I upvote. – D_Serg Apr 07 '20 at 15:13
  • 1
    Geometric is just like an underrated actor in Bollywood, who can act really well but doesn't get enough exposure. – Laveena May 14 '23 at 17:56
  • [Clapping.] 2-norm looks in the most important direction, Frobenius looks in all directions (which is wiser). – Oskar Limka Oct 03 '23 at 09:25
  • @OskarLimka what do you mean by most important direction vs all directions? – nullspace Dec 29 '23 at 16:39
  • @nullspace 2-norm quantifies the direction and intensity of maximal stretching, Frobenius quantifies the square-mean of stretching over all directions. – Oskar Limka Jan 01 '24 at 20:28
24

See Wikipedia for all definitions. Take this matrix: $$ \begin{pmatrix} 2 & -1 \\ -1 & 2 \end{pmatrix} $$ Its Frobenius norm is $\sqrt{10}$, but its eigenvalues are $3,1$ so, if the matrix is symmetric, its $2$-norm is the spectral radius, i.e., $3$. The Frobenius norm is always at least as large as the spectral radius. The Frobenius norm is at most $\sqrt{r}$ as much as the spectral radius, and this is probably tight (see the section on equivalence of norms in Wikipedia).

Note that the Schatten $2$-norm is equal to the Frobenius norm.

ps3lister
  • 43
Yuval Filmus
  • 57,953
  • 1
    Ohh, I was just using the vector 2-norm (Euclidean norm) operation on the matrix, not the correct matrix 2-norm. The vector 2-norm (piecewise square, sum all elements, square root) when extended to a matrix would be the Schatten 2-norm I guess. – Ricket Apr 15 '11 at 02:15
  • I think you got the $\sqrt{r}$ bound backwards, no? –  Apr 15 '11 at 02:23
  • You're right. Corrected. – Yuval Filmus Apr 18 '11 at 18:20
  • 1
    Also, it is true that both bounds are tight: the former is attained by a matrix with all but one entries being zero; the latter is attained by the identity matrix. –  Apr 18 '11 at 18:36
6

The L2 (or L^2) norm is the Euclidian norm of a vector.

The Frobenius norm is the Euclidian norm of a matrix.

Jay Griff
  • 95
  • 1
  • 1