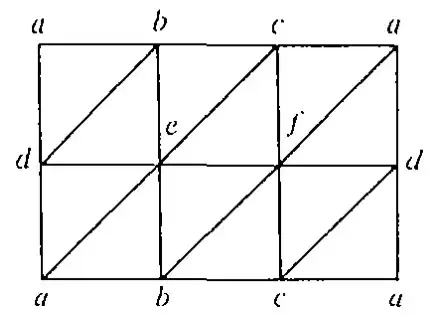
Why is the following triangulation not a simplicial complex for the torus?
Asked
Active
Viewed 326 times
2
-
1I think the problem is the 1-simplex [a, d]. Simplicial complexes need their simplices to be uniquely identifiable by their vertices. In this diagram it seems like the "top" [a,d] and the "bottom" [a, d] must be different, yet have the same vertex sets. – abhi01nat Jul 17 '19 at 08:36
-
Maybe related: https://math.stackexchange.com/questions/953586 and comments therein. – C.F.G Jul 17 '19 at 09:14
-
@AbhinavVNatarajan Thanks a lot. I understood. In the definition of a simplicial complex, the intersection of any two simplexes is a face of each of them but here the intersection of the top $[a,d]$ and the bottom $[a,d]$ is $a\cup b$ which is not a face of each of them. Is it true? – M.Ramana Jul 17 '19 at 10:27
-
@C.F.G Thank you for the comment. – M.Ramana Jul 17 '19 at 10:28
-
@M.Ramana I'm not sure I understand your question. The triangulation above is a valid simplicial complex, but is not a triangulation of the torus. The latter would require that the top and bottom halves of each vertical edge be distinct, which isn't the case here. – abhi01nat Jul 17 '19 at 19:10