How to use integrals to find the volume of the following ellipsoid? What are the associated parametric equations for this sort of ellipsoid?
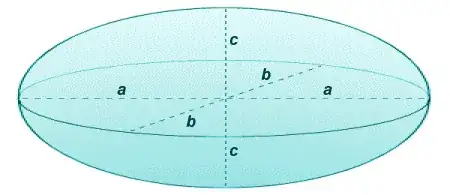
How to use integrals to find the volume of the following ellipsoid? What are the associated parametric equations for this sort of ellipsoid?

Since I don't know how much calculus you know, with a little intuition, you know all you really need to know if you just have some basic knowledge of integration, and substitution.
Consider the ellipse $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$ we have in particular $$ y = b \sqrt{1 - \frac{x^2}{a^2}}$$ so in particular the area of this ellipse is simply $$ A = 4\int_0^a b \sqrt{1 - \frac{x^2}{a^2}} \ \text{d}x $$ making the substitution $$ u = \frac{x}{a} $$ we have $$ x = au \Rightarrow \text{d}x = a \text{d}u$$ we get the area $$ A = 4ab \int_0^1 \sqrt{1-u^2} \ \text{d}u $$ we now substitute $$ u = \sin \theta$$ so that $$\text{d}u = \cos \theta \ \text{d}\theta $$ and we get $$ A = 4ab \int_0^{\pi/2} \cos^2 \theta \ \text{d}\theta $$ using the Pythagorean identity. With the substitution again $$ \phi = \frac{\pi}{2} - \theta$$ we get $$ A = - 4ab \int_{\frac{\pi}{2}}^0 \cos^2\left( \frac{\pi}{2} - \phi\right) \ \text{d}\phi$$ adding these two expressions together, we get $$ 2A = (4ab) \left(\int_0^\frac{\pi}{2} \cos^2(\theta) \ \text{d}\theta + \int_0^\frac{\pi}{2} \sin^2(\theta) \ \text{d}\theta \right) = 4ab\int_{0}^{\frac{\pi}{2}} \text{d}\theta = 2\pi ab \Rightarrow A = \pi ab$$
Okay, so the area of an ellipse is $\pi ab$, where $a$ and $b$ are the lengths of the semi-minor and semi-major axes. Equipped with the formula, we're going to use a double integral to find the volume, with the knowledge of how the inner integral evaluate, if you know what that means. If not, that's totally fine, because you don't really need that to understand what's going on. Really, if we continuously add up all of the areas of all of the little ellipses we get slicing along the $x$ axis as we go along the ellipsoid, we get the area of the ellipsoid. So if we have the ellipsoid $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1$$ If we pick some $x \in [-a^2, a^2]$, we get the $y$-$z$ trace $$ \frac{y^2}{\displaystyle\left(b \sqrt{1-\frac{x^2}{a^2}} \right)^2} + \frac{z^2}{\displaystyle\left(c \sqrt{1-\frac{x^2}{a^2}} \right)^2} = 1$$ well, we recognize that as an ellipse, just like above. So, it's area is just $$ \pi \left(b \sqrt{1-\frac{x^2}{a^2}} \right) \left(c \sqrt{1-\frac{x^2}{a^2}} \right) = \pi bc \left( 1 - \frac{x^2}{a^2}\right) $$ and if we add up all of these little areas over all of our values of $x$, we get the volume of the ellipsoid. This is just the integral $$ V = \int_{-a}^{a} \pi b c \left( 1 - \frac{x^2}{a^2} \right) \ \text{d}x$$ we now can make the substitution $$ u = \frac{x}{a}$$ when we have again that $$ \text{d}x = a \ \text{d}u $$ so that our volume becomes $$ V = \pi abc \int_{-1}^{1} 1 - u^2 \ \text{d}u $$ we can just compute the anti-derivative using the inverse of the power rule to get $$ \pi abc \left. \left[ u - \frac{u^3}{3} \right] \right|_{-1}^{1} = \pi abc \left[ \frac{2}{3} - \left(- \frac{2}{3} \right) \right] = \frac{4}{3}\pi abc$$ So the volume of this ellipsoid is just $$\boxed{\frac{4}{3}\pi abc} $$
Well, here's an approach on first principles and reasoning (rather than explicit integration) that might actually be instructive.
You know the volume of a sphere is $V = \frac{4 \pi}{3} r^3$.
So the three principle axes of a sphere are $a = b = c = r$.
So naturally, you might guess the volume of an ellipsoid is $V = \frac{4 \pi}{3} a b c$.
Clearly the volume must be linearly proportional to each principal axis.
Think about it...
you can do this in cartesian coordinates.
$\displaystyle \int_{-a}^a\int_{-b\sqrt{1-\frac{x^2}{a^2} }}^{b\sqrt{1-\frac{x^2}{a^2}}}\int_{-c\sqrt{1-\frac{x^2}{a^2} - \frac{y^2}{b^2}}}^{c\sqrt{1-\frac{x^2}{a^2} - \frac{y^2}{b^2}}} 1 \ dz \ dy \ dx$
It doesn't require anything more advanced that the trig substitutions you learned in calc 1.
Alternatively, you can convert to a modified spherical coordinate system.
$x = a\rho\cos\theta\sin\phi\\ y = b\rho\sin\theta\sin\phi\\ z = c\rho\cos\phi$
$\int_0^{2\pi}\int_0^{\pi}\int_0^1 abc\rho^2\sin\phi\ d\rho\ d\phi\ d\theta$