If I have two linked tori of equal size with $r_{\rm major} >> r_{\rm minor}$ that are tangent at one point, can one of the toruses be slightly rotated around the line through both centers without colliding? (the x-axis in the image)
I'm trying to figure out if a fully stretched chain of round links can be twisted at all without getting shorter, and once it does start getting shorter, how to calculate length as a function of twist angle.
Let me set $r=r_\text{major}$ and $\delta=r_\text{minor}$ and let $2a$ (with $a<r$) be the distance between the centres of the tori. If the tori are "orthogonal" to each other, then they are internally tangent for $a=r-\delta$.
We can set up a convenient coordinate system, such that the central circle of the first torus lies on the $x-y$ plane and is centred at $(0,0,0)$, while the second torus has its centre at $(2a,0,0)$ and its central circle lies on a plane passing through the $x$-axis, forming with the $x-y$ plane a dihedral angle $\pi/2+\alpha$ (i.e. tori are orthogonal for $\alpha=0$). By symmetry, I will consider only the case $\alpha\ge0$. The central circles of the tori have then parametric equations given by: $$ (r\cos t,\ r\sin t,\ 0);\quad (2a-r\cos s,\ r\sin\alpha\sin s,\ r\cos\alpha\sin s). $$ The square of the distance between a point on the first circle and a point on the second circle is then a function $f(s,t)$ given by: $$ f(s,t)=4a^2-4ar(\cos s+\cos t)+2r^2(1+\cos s\cos t-\sin\alpha\sin s\sin t). $$ We can search for extrema of $f$ solving the equations $\partial f/\partial s=\partial f/\partial t=0$. It turns out that the minimum is at
$$ \cases{ s=t=0 & if $\displaystyle2{a\over r}\ge1+\sin\alpha$;\\ \displaystyle s=t=\pm\arccos{2a/r\over1+\sin\alpha} & if $\displaystyle2{a\over r}<1+\sin\alpha$.\\ } $$
Minimum distance is $2(r-a)$ in the first case and $$ \sqrt{2r^2(1-\sin\alpha)-4a^2{1-\sin\alpha\over1+\sin\alpha}} $$ in the second case.
Tori are tangent and don't overlap only if that minimum distance is equal to $2\delta$. Hence we find that half the distance between the centres of the tori is given by
$$ \cases{ a=r-\delta & for $0\le\sin\alpha\le1-2\delta/r$; \\ \\ \displaystyle a=\sqrt{r^2\cos^2\alpha-2\delta^2(1+\sin\alpha)\over2(1-\sin\alpha)} & for $1-2\delta/r<\sin\alpha\le \sqrt{1-4\delta^2/r^2}$. \\ } $$ The bound $\sin\alpha\le\sqrt{1-4\delta^2/r^2}$ (i.e. $\cos\alpha\ge2\delta/r$) is necessary to ensure that $a\ge\delta$ (for $a<\delta$ the tori would overlap). The limiting value $$\alpha_\max=\arccos{2\delta\over r}$$ represents then the maximum possible twist between two consecutive rings of the chain (see also the EDIT below).
In conclusion, a twisted chain gets shorter by the amount $2(r-\delta-a)(n-1)$, where the value of $a$ must be computed as above and $n$ is the number of rings in the chain.
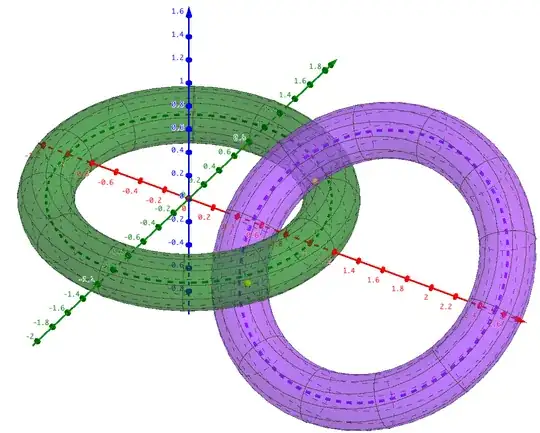
In the figure below you can see two linked tori, with $\delta/r=0.2$, twist angle $\alpha=50°$ and tangency points in yellow.
EDIT.
After I had completed this answer I found this paper which deals with the limiting case $\alpha=\alpha_\max$ (see figure below). The author shows that in such case the tori touch each other not only at two points, but all along a closed curve. In addition, the central circle of each torus is a Villarceau circle of a torus having the same central circle as the other torus but minor radius $2\delta$.
