Minimum of the Gamma Function $\Gamma (x)$ for $x>0$. How to find $x_{\min}$?

Question

The $\Gamma (x)$ function has just one minimum for $x>0$ . This result uses some properties of the gamma function:

• $\Gamma ^{\prime \prime }(x)>0$ and $\Gamma (x)>0$ for all $x>0$
• $\Gamma (1)=\Gamma (2)=1$.

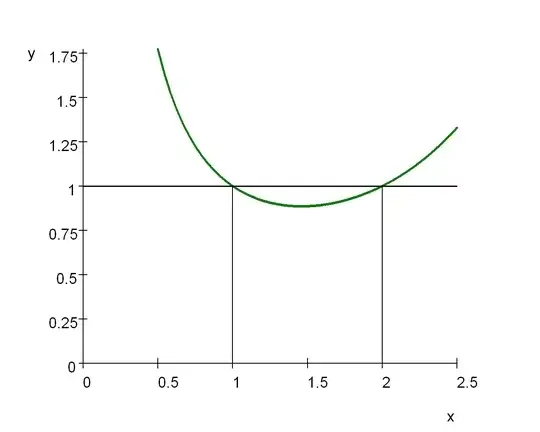
Observing the following graph (created in SWP) of $y=\Gamma (x)$ this minimum is near $x=3/2$, but likely $\min \Gamma (x)\neq \Gamma \left( 3/2\right) =\dfrac{1}{2}\Gamma \left( 1/2\right) =\dfrac{1}{2}\sqrt{\pi }$.

I think that it is not possible to find analytically the exact value of $x_{\min }$, even by converting to an adequate problem in the interval $]0,1]$ and using the functional equation $\Gamma (x+1)=x\Gamma (x)$ and the reflection formula

$\Gamma (p)\Gamma (p-1)=\dfrac{\pi }{\sin px}\qquad $( $0\lt p\lt 1$)

Question:

a) Which is the best way to find $\min_{[1,2]}\Gamma (x)$ and does $x_{\min }$ lay in $[1,3/2]$ or in $[3/2,2]$?

b) Is there some useful series expansion of $\Gamma (x)$?

c) Which numeric method do you suggest?

---

Edit: Due to the shape of $\Gamma (x)$ I thought on the one-dimensional Davies-Swann-Campey method of direct search for unconstrained optimization, which approximates a function near a minimum by successive approximating quadratic polynomials.

Answer 1

You have $$\frac d {dx} \Gamma(x)=\Gamma (x)\, \psi (x)$$ Knowing that the solution is close to $\frac 32$, make a Taylor expansion around this value. This would give $$y=\psi (x)=\psi^{(0)} \left(\frac{3}{2}\right)+\left(\frac{\pi ^2}{2}-4\right) \left(x-\frac{3}{2}\right)+\frac{1}{2} \psi ^{(2)}\left(\frac{3}{2}\right)\left(x-\frac{3}{2}\right)^2+O\left(\left(x-\frac{3}{2}\right)^3\right)$$ Now, using series reversion $$x=\frac{3}{2}+t-\frac{ \psi ^{(2)}\left(\frac{3}{2}\right)}{\pi ^2-8}t^2+O\left(t^3\right)\qquad \text{where} \qquad t=\frac{y-\psi ^{(0)}\left(\frac{3}{2}\right)}{\frac{\pi ^2}{2}-4}$$ Making $y=0$ gives $t=-\frac{2 (2-\gamma -2 \log (2))}{\pi ^2-8}$ leading to the estimate $$x\sim\frac 32 +\frac{2(\gamma +2 \log (2)-2)}{\left(\pi ^2-8\right)^3} A$$ where $$A=28 \zeta (3) (\gamma +2 \log (2)-2)+128-32 \gamma -16 \pi ^2+\pi ^4-64 \log (2)$$ $$x \approx 1.461632068$$ while the "exact" solution is $1.461632145$.

Answer 2

There indeed is no closed-form for the gamma function's minimum; what you can do instead, however, is to find the positive root of the digamma function (the logarithmic derivative of the gamma function), which should be available in your computing environment.

Answer 3

According to MathWorld the minimum of the Gamma function for positive $x$ is 1.46163...; in particular I guess this is enough to deduce that it is smaller than $3/2$. You can follow the links along to find some references where this is proved.

Answer 4

By Lagrange inversion theorem on the series definition of Digamma function $$\psi^{-1}(z)=\frac32+\frac{2}{\pi^2-8}(z-2+\gamma+\ln4)+\frac{8(7\zeta(3)-8)}{(\pi^2-8)^3}(z-2+\gamma+\ln4)^2+\left(\frac{64(7\zeta(3)-8)^3}{(\pi^2-8)^5}-\frac{8(\pi^2-96)}{3(\pi^2-8)^4}\right)(z-2+\gamma+\ln4)^3+\left(\frac{640(7\zeta(3)-8)^3}{(\pi^2-8)^7}+\frac{160(7\zeta(3)-8)(\pi^4-96)}{3(\pi^2-8)^6}+\frac{32(31\zeta(5)-32)}{(\pi^2-8)^5}\right)(z-2+\gamma+\ln4)^4+....$$ Hence, $x_{\min}=\psi^{-1}(0)\approx 1.4616321$ thanks to WA.

Answer 5

Looking for the zero of the digamma function, let $x_0=\frac 32$ and use the $\color{red}{\text{first iteration}}$ of Newton-like methods of order $n$. The obtained expression of $x_1$ is $\color{red}{\text{fully explicit}}$.

Converted to decimals $$\left( \begin{array}{ccc} n & \text{first iterate for order } n & \text{method} \\ 2 & \color{red}{1.46}09650320064341086 & \text{Newton} \\ 3 &\color{red}{1.46162}90121170218466 & \text{Halley} \\ 4 &\color{red}{1.4616321}028515388221 & \text{Householder} \\ 5 &\color{red}{1.461632144}2852193151 & \text{no name} \\ 6 &\color{red}{1.4616321449}563980751 & \text{no name} \\ 7 &\color{red}{1.461632144968}1447118 & \text{no name} \\ 8 &\color{red}{1.4616321449683}583003 & \text{no name} \\ 9 &\color{red}{1.461632144968362}2653 & \text{no name} \\ 10 &\color{red}{1.4616321449683623}398 & \text{no name} \\ \cdots&\cdots& \cdots \\ \infty& \color{red}{ 1.4616321449683623413} & \text{solution} \\ \end{array} \right)$$

Answer 6

Similar to @ClaudeLeibovici :

Define $0<x<1$:

$$f\left(x\right)=\left(\int_{0}^{\infty}e^{-y^{2}}dy-x!\right)$$

Then $f(x_1)=0,f(0.5)=0$ now take the arithmetic mean of $x_1,0.5$ and before use Newton's method to evaluate $x_1$ with as starting value $\sqrt{2}-1$ with some iterations and proceed the same further. Now we have the $x_{min}$ .

Answer 7

Too long for a comment :I have a start of a series for the minimum of the Gamma function :

Let $x>0$ consider :

$$f\left(x\right)=\frac{1}{3}\cdot\frac{1}{\sin\left(x\right)\left(1-\sqrt{x}\right)+1}+\frac{2}{3}\left(\frac{1}{\sin\left(x\right)\left(1-x\right)+1}\right)^{\frac{3}{5}}+\frac{1}{1400}\left(1-\sqrt{1+x\left(1-x\right)}\right)-\frac{1}{19000}\left(1-\sqrt{1+x\left(1-x\right)}\right)^{2}$$

Then :

$$f'\left(0.461632144\right)<8*10^{-9}$$

Now define :

$F\left(x\right)=\frac{1}{3}\cdot\frac{1}{\sin\left(x\right)\left(1-\sqrt{x}\right)+1}+\frac{2}{3}\left(\frac{1}{\sin\left(x\right)\left(1-x\right)+1}\right)^{\frac{3}{5}}+\frac{1}{1400}\left(1-\sqrt{1+x\left(1-x\right)}\right)-\frac{1}{19000}\left(1-\sqrt{1+x\left(1-x\right)}\right)^{2}+\cdots+a_n\left(1-\sqrt{1+x\left(1-x\right)}\right)^{n}+\cdots$

Then it seems there exists $a_n\in(-\infty,\infty)$ such that (denotes $y=0.4616$ the minima of the factorial function over the postive real axis)

$$F'(y)=0$$

Edit :

Compare $f(x)$ with $x\in(0,1)$ :

$$h\left(x\right)=\sqrt{\frac{x!}{\left(2-x!!\right)^{2}\left(2-x!!!\right)^{2}\left(2-x!!!!\right)^{2}\left(2-x!!!!!\right)^{2}\cdot\cdot\cdot}}$$

Where $\Gamma(x+1)=x!,\Gamma(1+\Gamma(x+1))=x!!,\cdots$

Conjecture :

$\exists a,b>0,n,p\in N^+$ such that as $p\to \infty$ :

$$\left(\sum_{n=1}^{p}\frac{\left(1-x\left(\frac{1}{bn}-\frac{x}{bn}\right)^{n}\right)}{p}\right)^{a}\to x!,x\simeq 0.4616321944$$