"implied multiplication" operator precedence?

Question

I hold a masters in computer science from one of the worlds top universities and until today I thought I more or less know basic math.

I'm sure you guys all know these click-bait simple "90% of people can't solve this equation" posts on facebook where everyone starts to argue over a simple equation (and I DEFINITELY don't want to kick off one of those - but I'd like to discuss the roots of this confusion).

So today there was another one of those:

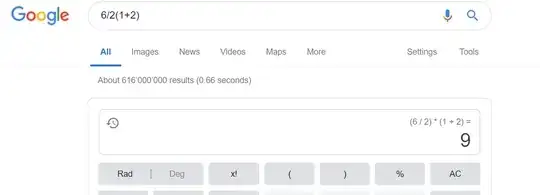
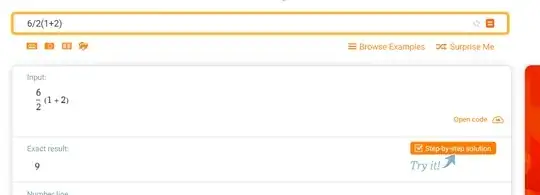
6/2(1+2)

Based on what I learned and applied throughout all my years in university, this equals 9, since brackets are evaluated first and then it's left to right, since division and multiplication have the same operator precedence.

Google agrees with that:

Wolfram Alpha agrees with that:

and my texas instruments agrees with that too. So it's 9, right?

Well today I came across a claim I hadn't heard before, which is "implied multiplication takes precedence over both explicit multiplication and division" - so by that rule it would not be left to right in the above example, but the implied multiplication would be evaluated before the division, which would mean that

6/2(1+2) == 1 != 6/2*(1+2)

So, are google, wolfram alpha and my calculator all wrong (they by the way also yield 9 if ÷ is used instead of /)?

The only thing i found on the issue so far is this statement on Wikipedia (https://en.wikipedia.org/wiki/Order_of_operations):

Mixed division and multiplication: Similarly, there can be ambiguity in the use of the slash symbol / in expressions such as 1/2x.[5] If one rewrites this expression as 1 ÷ 2x and then interprets the division symbol as indicating multiplication by the reciprocal, this becomes:

1 ÷ 2 × x = 1 × 1/2 × x = 1/2 × x.

With this interpretation 1 ÷ 2x is equal to (1 ÷ 2)x.1[6] However, in some of the academic literature, multiplication denoted by juxtaposition (also known as implied multiplication) is interpreted as having higher precedence than division, so that 1 ÷ 2x equals 1 ÷ (2x), not (1 ÷ 2)x. For example, the manuscript submission instructions for the Physical Review journals state that multiplication is of higher precedence than division with a slash,[7] and this is also the convention observed in prominent physics textbooks such as the Course of Theoretical Physics by Landau and Lifshitz and the Feynman Lectures on Physics.[a]

So one thing this tells me is clearly AVOID IMPLIED MULTIPLICATION

but what is internationally actually 'more correct and less wrong'? Also, I don't fully see how ÷ vs. / is relevant to this question?

By the way, some calculators do seem to evaluate to 1:

Answer 1

While the rules of mathematics are usually very precise, this is more of a grammar issue. Once the written form is correctly parsed, then you can apply precise and well-known rules to solve it. The problem is that there's no consensus on the right way to parse implied multiplication in the context of a larger expression.

There's a good analysis here, in which the author basically asserts that both answers are right, and the question is wrong.

My personal theory is that because many of us see polynomial terms as being discrete things, we tend to treat similar structures in other places as being discrete. When I see something that looks like a polynomial term, my inclination is to treat it as if it has parentheses around it. So, I see 2/4x as 2/(4*x), while others may see (2/4)*x. Both interpretations can be found in different textbooks.

You could avoid the ambiguity by rewriting the question without implied multiplication. An even better approach would be to change the way you represent division, and put the numerator above the denominator.

Answer 2

I've seen many of these clickbait problems on Facebook. Sometimes they add extra operators, but it always boils down to how you interpret an expression of the form a/bc. This doesn't have a widely agreed-upon answer because it's just not a part of formal mathematical notation.

• In proper mathematical typesetting, you'd use fraction notation, and thus write $\frac{a}{bc}$ or $\frac{a}{b} c$, depending on the intended meaning. The top and bottom sides of the fraction bar serve as implicit grouping brackets, so $\frac{N}{D} = \frac{(N)}{(D)} = (N) / (D)$. There is no ambiguity.
• In most computer programming languages, implicit multiplication isn't allowed (mainly because this would prevent having descriptive multi-letter variable names). You have to write a/(b*c) or a/b*c, with an explicit * for multiplication. The latter form is parsed as (a/b)*c due to the rule of left-to-right evaluation of * and / operators (which are at the same precedence level). So again, no ambiguity.

Ambiguity shows up when expressions are typed in a “linear” format (with division written as $a/b$ or $a \div b$, instead of as $\frac{a}{b}$) while also using implicit multiplication ($bc$ instead of $b \times c$, $b \cdot c$, or $b * c$). There are two main schools of thought on operator precedence (often inaccurately called “order of operations”). One is the familiar PEMDAS:

1. Parentheses
2. Exponentation (right to left)
3. Multiplication and Division (left to right)
4. Addition and Subraction (left to right)

The other is PEJMDAS, which breaks out juxtaposition (implicit multiplication) into its own level.

1. Parentheses
2. Exponentation (right to left)
3. Juxtaposition
4. (explicit) Multiplication and Division (left to right)
5. Addition and Subraction (left to right)

There really isn't a strong argument for preferring one to the other.

• The main argument for PEMDAS, which interprets a/bc as (a/b)c, is that it treats explicit and implicit multiplication uniformly, thus making things easier for compiler developers.
• The main argument for PEJMDAS, which interprets a/bc as a/(bc), is that bc being written as one “word” just makes it look more tightly bound as a unit than an operation written with punctuation. This is especially true when spaces are added in a / bc.

As you have noted, both interpretations are used by various calculators and computer algebra systems. So what should you do?

“Doctor, it hurts when I do this.”
“Then don't do that.”

Make a habit of never writing $a/bc$. Always explicitly disambiguate between $(a/b)c$ and $a/(bc)$. And when someone else asks a math question with $a/bc$, ask them to clarify.

---

As for why the confusion occurs, I think it's a educational issue. When students are first introduced to multiplication in elementary school, it's always using an explicit operator (usually $\times$): $2 \times 2 = 4$, $7 \times 8 = 56$, etc. Only when they get to (pre-)algebra, with its concept of “variables”, is implicit multiplication introduced. “Hey, it's getting annoying to use all these $\times$'s, so from now on let's just write $ab$ instead of $a \times b$.” But then they never go back and revisit Aunt Sally to see how she likes this new type of multiplication.

Perhaps we should change the mnemonic to replace the term “parentheses” with “grouping”. The “grouping” symbols will of course include parentheses (...) and the similar bracket pairs [...] and {...}. But it also includes “hidden” grouping brackets in notations like fractions ($\frac{a}{b} = \frac{(a)}{(b)}$) and radicals ($\sqrt{x} = \sqrt{(x)}$). And when implicit multiplication is introduced, let's ask: Does juxtaposition count as “grouping”?

Answer 3

In your picture of the $2$ calculators the one with the $9$ answer was only programed for order of operations. The calculator with the answer of $1$ was also programed to consider the distributive property. A calculator is only as good as its programming and only as intelligent as its user.

When I went to school we were taught implied multiplication took precidence because of the distributive property. And the order of operations was a suggestion not concrete.

Answer 4

@Robert w Shull is correct,

Implied multiplication in this instance comes from the Distributive Law.

Distributive law, in mathematics, the law relating the operations of multiplication and addition, stated symbolically, a(b + c) = ab + ac; that is, the monomial factor a is distributed, or separately applied, to each term of the binomial factor b + c, resulting in the product ab + ac.

–Encyclopedia Britannica

Because Parenthesis have the highest priority in the order of operations, the equation is correctly solved as follows:

6÷2(1+2)=?
6÷(2*1 + 2*2)=?
6÷(2 + 4)=?
6÷(6)=?
6÷6=1

Because there is only one "explicit" operator (division) outside of the parenthetical term, the equation is a simple fraction...

$$ \frac{6}{2(1+2)}$$

which we can then reduce... $$ \frac{3}{(1+2)}$$

finally... $$ \frac{3}{3}=1$$

Updated: Implied multiplication is everywhere, 1x = x and x/1=x. Any number times 1 is that number and any number divided by 1 is that number. We can use this fact to maintain that the given equation is an implicit explicit division problem.

6÷2(1+2)=?
3÷1(1+2)=?
3÷1(3)=?
3÷3=1

More support here:https://producers.wiki/wiki/The_equation_that_broke_the_Internet

Answer 5

The problem lies with the current definition of what constitutes a term or rather, what separates a term. In my time we learned terms were separated by any operator. Today they are teaching only [+ or -] So now they take things in bigger bites. I believe this loses the minutia of things. 6 / 2(1+2) I see as plainly two terms so left divided by right. But there is no + or - not enclosed in parenthesis so to the new definition it is one term. So they do not know where to start and instead of starting with the parenthesis just go L to R and associate the 2 with the division rather that the parenthesis. They also see 2x3 and (2x3) both to be one term. But then they see 6/2x3 as three operations but 6/(2x3) as two operations, they do not see the inconsistency here. So you see my concern with only + or - separating terms. Is this the basis for dyscalculia suffered by many young people trying to learn math. ?? Well if you don't know what constitutes a term, I couldn't think you would go far.

My responder says I need to provide references and footnotes for my observations to be true. WOW, I have seen this discussion on YouTube and from the many conversations I have read, I have reached this conclusion. I have watched this thread for several years. People who properly define terms get one answer and people who do not get the other answer. By properly I mean ALL operators separate terms. [As per the understanding of my generation, I'm 73]

I have been told that 2(3)=2x3 and also that 2x3 and (2x3)are both one term and both are the same.

I also see it being taught that (2x3)=2x3=6 Instead of (2x3)=(6)=6 Sorry but folks of my generation have NOT been taught to see (2x3) as being the same as 2x3. I doubt anyone has written a book about this. Maybe they should.

As for my qualifications to make these observations, I do have a BSEE and attended a prestigious university. Is that good enough, Mr Stucky?