6

Given two circles (defined by center and radius), how do I find the smallest ellipse that encloses both of them? I.e. I search the green ellipse in the picture below.

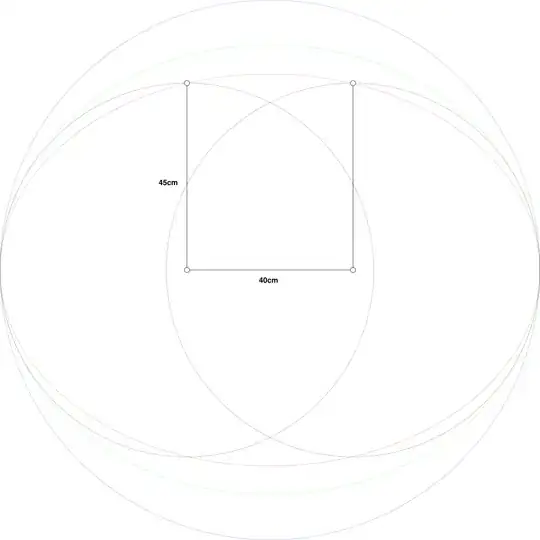
enter image description here

The ellipses can be considered axes aligned if this simplifies things. The end goal is to classify points on whether they are in the ellipse or not. So a final representation suitable to the form used in this question will be preferred.

Community
  • 1
fho
  • 183
  • What do you mean by the smallest? Are you considering the area, or maybe the larger radius or maybe perimeter or yet something else? – dtldarek Mar 06 '13 at 08:42
  • Are the radii of the two circles the same? – Christian Blatter Mar 06 '13 at 09:06
  • @ChristianBlatter: They are not necessarily the same. – fho Mar 06 '13 at 09:42
  • @dtldarek: The one with the smallest minor axis with only two intersection points on the circles. – fho Mar 06 '13 at 09:43
  • The minor axis doesn't seem to be an interesting quantity to minimize: The minimal possible value of the minor axis is the radius of the larger circle; and when both circles have the same radius, the ellipse will be infinite then.– When you want to minimize the area there will be many cases, depending on the radii of the two circles and the distance of their centers. – Christian Blatter Mar 06 '13 at 20:25

2 Answers2

1

Join the two centers and extend the line. wherever it cuts the two circles at their outer extremes are the points which are crucial say $A$ and $B$. take the mid point of these two points. for simplicity consider this point as the origin.

now consider an ellipse with the major axis as the line segment $AB$ and call this as $x$-axis. you need to find the minor axis and you are done. the equation of an ellipse is

$$\frac{x^2}{a^2}+\frac{y^2}{b^2} = 1$$

here $a$ is known and $b$ is to be found. find the radius of the osculating circle of this ellipse at the points $A$ and $B$, which is of course the same numerical value (why?)

then equate this numerical value to the maximum of the two radii. this will give you an equation in $b$ which you can solve.

magguu
  • 300
  • @Florian The curvature of an ellipse can be found here (search for "The curvature and tangential angle of the ellipse are given by"). – dtldarek Mar 06 '13 at 08:58
  • I am not sure I understand the "then equate this numerical value" part. Given the equation I can solve for b, use the numerical value as a and one of the intersection points as (x,y). Will this give me the smallest b? Or am I mistaken here? – fho Mar 06 '13 at 10:35
  • i wanted to give this as an exercise as the computations are a bit cumbersome to write. do u know what an osculating circle is ? to find it you need to consider the distance parametrized curve ...

    tell me if you do not understand all this i will explain in a new answer

     – magguu Mar 06 '13 at 15:03
  • @magguu: I don't :) ... but it would be great if you could point me to some material on it. I have another project that might benefit from this. – fho Mar 07 '13 at 11:12
  • @Florian There are many excellent books. You may refer to the first chapter of doCarmo, Differential Geometry of Curves and Surfaces. – magguu Mar 07 '13 at 12:11
  • @magguu Sadly that book is not available in our library. Could you please explain what you mean by "equate this value to the maximum"? How will equating two values give me an equation? – fho Mar 11 '13 at 14:05
  • you already know the two radiis $r$ and $R$. the radius of the osculating circle of the ellipse at the point $(a,0)$ will give an expression in $a$ and $b$. here $a$ is known. equate this expression to $R$. this gives you an equation in $b$, which you can solve. – magguu Mar 11 '13 at 19:45
  • @Florian You may also look in - Montiel and Ross

    sorry I am not able to recall any more books at the moment. but this is a very basic topic and many lectures notes are available in home pages of many professors. just do a google search.

     – magguu Mar 12 '13 at 04:45
0

try and place this on the center of cartesian plane. you will see that equation for the ellipse enclosing is $$\frac{x^2}{(10+45)^2} + \frac{y^2}{b^2} = 1$$ and the one of the two smaller ellipses that are being enclosed is $$\frac{(x-10)^2}{45^2} + \frac{(y-0)^2}{40^2} = 1$$ and the other one is $$\frac{(x+10)^2}{45^2} + \frac{(y-0)^2}{40^2} = 1$$

Ignore one the second equation (since if it encloses the first one, it will enclose the second) and now find the intersection between the enclosing ellipse and the enclosed ellipse.

How to find this intersection? just rearrange both equations 1 and 2 till it looks like this $$y^2=...$$ Equate both the equations and try and rearrange till it looks like a quadratic equation with your unknown $b$ as coefficients essentially like this $$0=()x^2+()x+()$$ with all your $b$'s inside those brackets

now why did we try to find the intersection initially? The reason was to ensure that we only have 1 intersection between the ellipses, located on the x-axis, tangential to each other at the edge.

This condition is set so that if we have more intersections, we know that its not going to enclose, rather cut through the ellipses midway.

How do we express mathematically, through the discriminant and set =0 so only 1 solution, or intersection. $$B^2-4AC=0$$ A stands for the stuff within the bracket of$()x^2$

B stands for the stuff within the bracket of$()x$

C stnads for the stuff within the bracket of$()$ at the end

input values and solve for b, now all that's left is putting this into the original equation, and congrats! you have found the solution!

ruby duby
  • 129