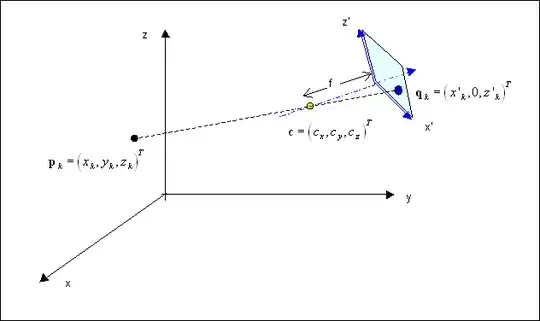
Taking a geo and camera reference systems as shown in the sketch, with an evident meaning of the various terms,
we may consider that, prior to translation, the camera is rotated around the $z$ axis by an angle $\gamma$, and then
by an angle $\alpha$ around the new axis $x'$.
The two angles are taken according to the right-hand rule, and will be normally small.
Therefore we have that the new unit vectors will have coordinates
$$
\left( {{\bf i'}\,|\,{\bf j'}\,|\,{\bf k'}} \right) = {\bf R}_{\,{\bf x'}} (\alpha ){\bf R}_{\,{\bf z}} (\gamma )\left( {{\bf i}\,|\,{\bf j}\,|\,{\bf k}} \right)
= {\bf R}_{\,{\bf z}} (\gamma ){\bf R}_{\,{\bf x}} (\alpha )\left( {{\bf i}\,|\,{\bf j}\,|\,{\bf k}} \right)
$$
where
$$
{\bf R}_{\,{\bf x}} (\alpha ) = \left( {\matrix{
1 & 0 & 0 \cr 0 & {\cos \alpha } & { - \sin \alpha } \cr 0 & {\sin \alpha } & {\cos \alpha } \cr } } \right)
\quad
{\bf R}_{\,{\bf z}} (\gamma ) = \left( {\matrix{
{\cos \gamma } & { - \sin \gamma } & 0 \cr {\sin \gamma } & {\cos \gamma } & 0 \cr 0 & 0 & 1 \cr } } \right)
$$
A (vertical) vector fixed in the geo-reference will tranform in the inverse way
$$
\left( {\matrix{ {x'} \cr {y'} \cr {z'} \cr } } \right)
= {\bf R}_{\,{\bf x}} ^{\, - \,{\bf 1}} (\alpha ){\bf R}_{\,{\bf z}} ^{\, - \,{\bf 1}} (\gamma
)\left( {\matrix{ x \cr y \cr z \cr } } \right)
= {\bf R}_{\,{\bf x}} ( - \alpha ){\bf R}_{\,{\bf z}} ( - \gamma )
\left( {\matrix{ x \cr y \cr z \cr } } \right)
$$
We have then to add a translation vector
$$
\left( {\matrix{ {x'} \cr {y'} \cr {z'} \cr } } \right)
= {\bf R}_{\,{\bf x}} ( - \alpha ){\bf R}_{\,{\bf z}} ( - \gamma )
\left( {\left( {\matrix{ x \cr y \cr z \cr } } \right)
- \left( {\matrix{ {s_{\,x} } \cr {s_{\,y} } \cr {s_{\,z} } \cr } } \right)} \right)
$$
such that
$$
\eqalign{
& \left( {\matrix{ 0 \cr { - f} \cr 0 \cr } } \right)
= {\bf R}_{\,{\bf x}} ( - \alpha ){\bf R}_{\,{\bf z}} ( - \gamma )
\left( {\left( {\matrix{ {c_{\,x} } \cr {c_{\,y} } \cr {c_{\,z} } \cr } } \right)
- \left( {\matrix{ {s_{\,x} } \cr {s_{\,y} } \cr {s_{\,z} } \cr } } \right)}
\right)\quad \Rightarrow \cr
& \Rightarrow \quad \left( {\matrix{ {s_{\,x} } \cr {s_{\,y} } \cr {s_{\,z} } \cr } } \right)
= \left( {\matrix{ {c_{\,x} } \cr {c_{\,y} } \cr {c_{\,z} } \cr } } \right)
+ {\bf R}_{\,{\bf z}} (\gamma ){\bf R}_{\,{\bf x}} (\alpha )
\left( {\matrix{ 0 \cr f \cr 0 \cr } } \right)\quad \Rightarrow \cr & \Rightarrow \quad {\bf s}
= {\bf c} + f\,{\bf n} \cr}
$$
The line from $\bf p_k$ through $\bf c$ has equation
$$
{\bf x} = {\bf p}_{\,k} + \lambda _{\,k} \left( {{\bf c} - {\bf p}_{\,k} } \right)
$$
which in the camera reference translates into
$$
\eqalign{
& {\bf x}' = {\bf R}_{\,{\bf x}} ( - \alpha ){\bf R}_{\,{\bf z}} ( - \gamma )\left( {{\bf x} - {\bf s}} \right) = \cr
& = {\bf R}_{\,{\bf x}} ( - \alpha ){\bf R}_{\,{\bf z}} ( - \gamma )\left( {{\bf p}_{\,k} + \lambda _{\,k} \left( {{\bf c} - {\bf p}_{\,k} } \right) - {\bf s}} \right) = \cr
& = {\bf R}_{\,{\bf x}} ( - \alpha ){\bf R}_{\,{\bf z}} ( - \gamma )\left( {\left( {\lambda _{\,k} - 1} \right)\left( {{\bf c} - {\bf p}_{\,k} } \right) - f\,{\bf n}} \right) = \cr
& = \left( {\lambda _{\,k} - 1} \right){\bf R}_{\,{\bf x}} ( - \alpha ){\bf R}_{\,{\bf z}} ( - \gamma )\left( {{\bf c} - {\bf p}_{\,k} } \right) - \left( {0,f,0} \right)^{\,T} = \cr
& = {\bf q}_{\,k} = \left( {x'_{\,k} ,0,z'_{\,k} } \right)^{\,T} \cr}
$$
and $\lambda _{\,k} $ shall be such as to render the $y'_{\,k}$ coordinate null.
In conclusion, we have as unknown the two angles $\alpha, \, \gamma$, the three components of $\bf c$, and if it is unknown, $f$.
Each couple of corresponding points will provide two equations (net of of the introduction of the further unknown $\lambda _{\,k} $).
We need therefore at least three couples of corresponding points.
To counterbalance the error/indetermination in the coordinates the addition of further points
will be beneficial and can be dealt by Least Square Error methods.


