2

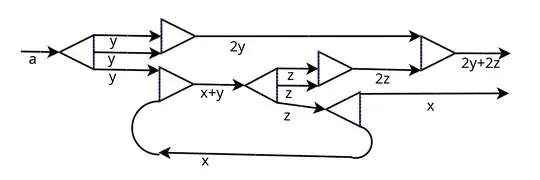
I'm currently playing the game Satisfactory, where I need to balance the conveyor belts to ensure a 100% efficient factory.

To help me in this job I have Merger and Splitter. The Splitter can split belts into 2 or 3 conveyor belts and the Merger can join 2 or 3 belts into one.

Now I have a certain Input of N Ressources and want 1/15 of N Ressources at the End. Which is the amount of Splitter and Merger I need for this problem and how can I calculate, if it is even possible to achieve 1/15 or other fractures.

Hope somebody can help me with this problem.

Christopher
  • 55
  • Seems like, based on what you described, you could just split $1$ belt into $2$, those into $4$, those into $8$, and then those into $16$, and then from there merge any pair to obtain a total of $15$ belts. Not sure if that's what you meant by all this though, seems a little too easy. – PrincessEev May 05 '19 at 21:45
  • No I Dont want 15 belts. I want the ressources from one belt split in a way, that I have 1/15 fraction of that resource again on one belt. – Christopher May 05 '19 at 21:47
  • 3
    It's enough to do a 1/5, then split each output into threes. You can do a 1/5 splitter like this: https://imgur.com/a/8YecreR – Jane Doé May 05 '19 at 22:11
  • @JaneDoé That doesn't work. You are using round-off. You can never get $\frac{1}{15}$ from that procedure. Mark Bennet's answer is correct. Even with feedback every output of every branch has a denominator equal to $2^m3^n$ for some non-negative $m$ and $n$. When you add such branches, the denominator retains its form so you can never achieve a $\frac{1}{15}$ split. – John Douma May 24 '25 at 17:03

2 Answers2

5

Here's how I did it.

enter image description here

$ 14 \over 15 $ out on the left $ 1 \over 15 $ out on the right

It does a divide by 5 in the three blocks on the right and a divide by three in the top block

The divide by 5 is achieved by dividing by 6 but feeding one of the sixths back into the input,

Given that is is possible to divide by 6 and to add this expression is allowed

$ x = {y+x \over 6} $

Then this simplifies via

$ 6x = y + x $

and

$ 5x = y $

to give the result:

$ x = {y \over 5 }$

Showing division by 5 is also possible. Precede a division by 5 with a division by 3 to get a division by 15

here it is again as a diagram.

enter image description here

it's easiest to start at the output with x, (mainly because I don't like dividing)

x is one half of z, so

z=2x

3z makes 6x

x+y=6x

y=5x

a=15x

Jasen
  • 223
  • Comments have been moved to chat; please do not continue the discussion here. Before posting a comment below this one, please review the purposes of comments. Comments that do not request clarification or suggest improvements usually belong as an answer, on [meta], or in [chat]. Comments continuing discussion may be removed. – Shaun May 28 '25 at 09:42
1

Look at the denominators. If you merge (add) two streams with denominators which have only prime factors $2$ and $3$ the sum has only prime factors $2$ or $3$ (some factor may cancel eg $\frac 12+\frac 12=1$).

Likewise if you split a fraction which has only prime factors $2$ or $3$ in the denominator into two or three equal pieces, the resulting fractions have only prime factors $2$ or $3$ in their denominators.

Therefore you can never get a fraction with $5$ in the denominator.

You can approximate $\frac 1{15}$ as closely as you like but can never get there exactly.

Mark Bennet
  • 101,769
  • 1
    What you're missing is that you can use feedback (so, merging the output with some of the input). You can do a 1/5 splitter like this for instance: https://imgur.com/a/8YecreR – Jane Doé May 05 '19 at 22:13
  • 3
    @JaneDoé I can see how to get a $\frac 15$ splitter with feedback as a limiting case (feedback 1/6 into the input of a three way splitter), and then it is trivial to get $\frac 1{15}$. But $\frac 1{15}$ is not attained exactly in finite time . OP doesn't talk about limiting processes of this kind. – Mark Bennet May 05 '19 at 22:24
  • OK! I wonder how the game handles the limiting process – Jane Doé May 05 '19 at 22:26
  • the splitters are deteministic (round robin) and the resources are discrete. it is achieved in finite time. – Jasen May 24 '25 at 14:29