Studying aspects of this problem I stumbled on this question.
Designating the golden ration by $\phi=\frac{1+\sqrt{5}}{2} \simeq 1.61803$ and letting
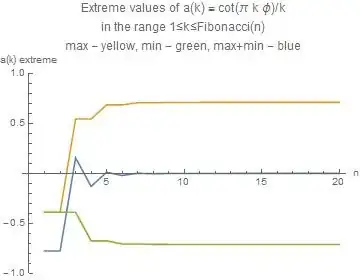
$$a(n) = \frac{1}{n} \cot(n \pi \phi)$$
(i) prove that $a(n)$ is bounded from above and from below
(ii) calculate $\max (a(n))$ and $\min (a(n))$ with $n =1,2,3,...$
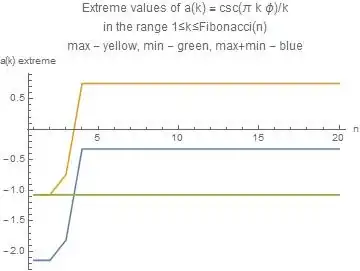
(iii) solve the similar problem when $\cot$ is replaced by $\csc$, i.e. consider
$$b(n) = \frac{1}{n \sin(\pi \phi n)}$$
In this case check the validity of my conjecture that $b(1)< b(n) < b(3)$ for $n\gt 3$
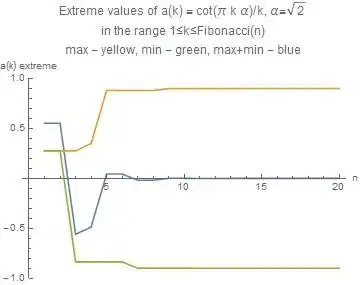
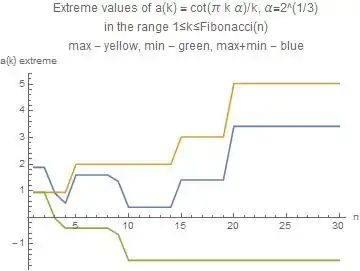
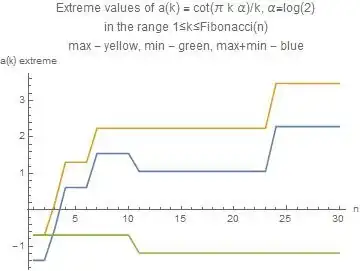
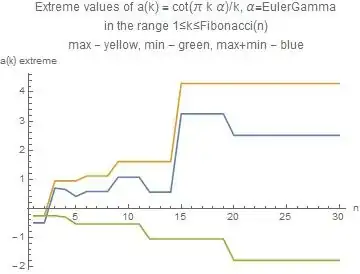
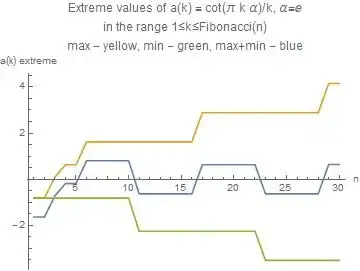
(iv) Extension: the same if $\phi$ is replaced by other irrational quantities like $\sqrt{2}$, $2^{\frac{1}{3}}$, $\log{2}$, $\gamma$, $\pi$, $e$. Here except for the case $\sqrt{2}$ I have no indication that the extremes exist at all, i.e. that $a(n)$ is bounded if $n \to \infty$.
What makes this question interesting (IMHO)?
One aspect is this:
The expression $b(n)$, when considered as a function of real $n\gt 0$ has simple poles at
$$n_{k} = k/ \phi, k=1,2,3,...$$
An integer $n$ can become very close to an $n_k$. I found it surprising that the rather modest damping factor $\frac{1}{n}$ is able to cancel the steep rise in the vicinity of the poles.
What have I done so far?
The modest part I did up to now is in the reference above. Addtionally here are graphs of the quantities in question. Remark: the choice of Fibonacci numbers as the upper limit of the range is made plausible in the quoted investigation.