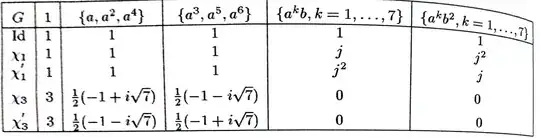
I am trying to understand the Characters table of non abelian group G of order 21.
In the attached picture, I understand how we get the 3 first irreducible representations of dimension 1. I guess we can get them by factorizing a morphism from G to $\Bbb C^*$ throug the quotient of G by its commutator H which is a Normal subgroup that we can identify with the 7-Sylow Normal group of G.
My question concerns the 3-dimentional representations. Getting one will help me get the other through orthogonality. I don't understand how we get $\chi_3$ for instance. Do we use a special morphism or a twist of other representations?
Thank you for your help.