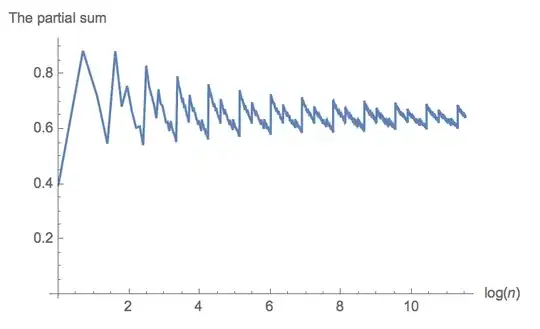
We prove the following.
Theorem
Let $\theta$ be an irrational number with bounded partial quotients, i. e. the simple continued fraction expansion $\theta=[a_0;a_1,a_2,\cdots]=a_0+\frac1{a_1+\frac1{a_2+\cdots}}$ satisfies $|a_i|\leq K$ for some absolute constant $K>0$. Then $$\lim_{n\rightarrow\infty}\frac1{n\log n}\sum_{k=1}^n |\cot \pi k \theta|=\frac 2{\pi}. $$
First, we need the lemma under the assumption that $\theta$ is an irrational number with bounded partial quotients. This is proved by basic properties of simple continued fraction.
Lemma
There is a constant $c=c(\theta)>0$ such that
$$
\left|\theta-\frac pq\right|\geq \frac 1{cq^2}. \ \ \ (1)
$$
Let $D_N$ be the discrepancy of the sequence $(k\theta)$, the fractional part of $k\theta$ modulo $1$, i. e.
$$
D_n:=\sup_{0\leq a\leq b\leq 1} \left|\frac1n \#\{1\leq k\leq n: (k\theta) \in (a,b) \} -(b-a)\right|.
$$
Then an important inequality for $D_n$ is also needed. This is Theorem 3.4 in Kuipers & Niederreiter 'Uniform Distribution of sequences'
Lemma
Let $\theta=[a_0;a_1,a_2,\cdots]$ be an irrational number with bounded partial quotients, say $|a_i|\leq K$. Then
$$
nD_n = O(\log n). \ \ \ (2)
$$
We also use Greg Martin's comment in the following form
$$
|\cot \pi x|=\frac1{\pi\|x\|}+O(1).$$
Now, split the interval $[0,1]$ into $h+2$ short intervals so that $h+2\asymp \frac n{\log^2 n}$, and
$$
\left[0,\frac{\log^2 n}n\right), \left[\frac{\log^2 n}n, \frac{2\log^2 n}n\right), \ldots, \left[\frac{h\log^2 n}n, \frac{(h+1)\log^2 n}n\right), \left[ \frac{(h+1)\log^2 n}n,1\right).
$$
Because we are computing $\|k\theta\|$, we only need the first half of these intervals.
By (2), for each $0\leq j\leq h$, the number $i_j(n)$ of elements in the sequence $(k\theta)$ that belongs to $[(j\log^2 n)/n, ((j+1)\log^2 n)/n)$, satisfies
$$
\left|i_j(n)- \log^2n \right|=O(\log n).
$$
From this and estimates by the right endpoints, we obtain the lower bound.
\begin{align}
\sum_{k=1}^n |\cot \pi k\theta| &= \sum_{k=1}^n \frac1{\pi\|k\theta\|}+O(n)\\
&\geq \frac2{\pi}\sum_{1\leq j\leq h/2} \frac n{j\log^2 n} (\log^2 n + O(\log n)) +O(n)\\
&\geq \frac2{\pi} n\log n + O(n\log\log n).
\end{align}
For the upper bound, we need a more precise estimate on the first short interval.
If $0\leq p < q \leq n$, the we have by (1),
$$
| (p\theta)-(q\theta)|\geq \frac 1{2cn}. \ \ \ (3)
$$
We split $[0, (\log^2 n)/n)$ into $t+2\asymp \log^2 n$ shorter intervals
$$
\left[0,\frac1{2cn}\right), \left[\frac1{2cn},\frac2{2cn}\right), \ldots, \left[\frac t{2cn}, \frac{t+1}{2cn}\right), \left[ \frac{t+1}{2cn},\frac{\log^2n}n\right).
$$
By (3), each interval contain at most one number of the form $(k\theta)$, with no such number lying in the first interval.
Then we have from the left endpoint estimates,
\begin{align}
\sum_{k=1}^n |\cot \pi k \theta |&=\sum_{k=1}^n \frac1{\pi\|k\theta\|}+O(n)\\
&\leq \sum_{j\leq 2c\log^2 n} \frac{2cn}j + 2\sum_{j\leq 1+h/2} \frac n{j\log^2 n}(\log^2 n + O(\log n)) + O(n)\\
&=\frac 2{\pi} n\log n + O(n\log\log n).
\end{align}
Hence, we obtain
$$
\sum_{k=1}^n |\cot \pi k \theta |=\frac2{\pi} n\log n+ O(n\log\log n).
$$