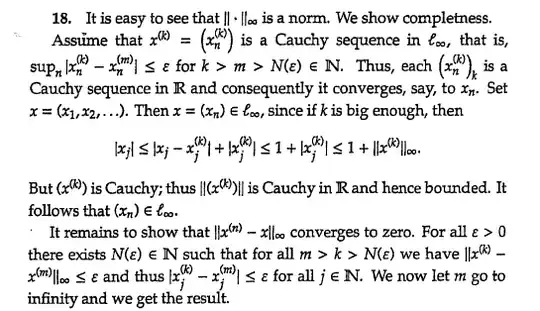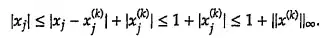I'm learning about Hilbert spaces and operators theory, from some book. I came across the following question -
And the books' answer:
What I don't understand in the proof -
Why can we understand that each sequence is Cauchy?
Moreover, why the following inequallity is true?