7

I'm a first year undergraduate student and I'm a math major. Currently, I'm taking an intro to analysis class and a linear algebra class. However, I often feel constrained by what I do in class and feel like exploring topics in math beyond class. I'm intrigued by topology but haven't had any prior exposure to it. At this stage, considering that my knowledge of both analysis and linear algebra is fairly elementary, does it make sense to delve into higher-level topics like topology? What are the pre-requisites for introducing oneself to topology? And if you recommend that I go on and try to self-learn some topology, what are some resources I can/should use?

In general, if not topology, at this stage, what beyond class can/should I do? Thanks!

Kaj Hansen
  • 33,511
gtoques
  • 1,484
  • 2
    Have you studied metric spaces? Understanding metric spaces well is essential before going into topology. If you have studied metric spaces then a good place to start studying topology is G F Simmon's 'Introduction to Topology and Modern Analysis' – Kavi Rama Murthy Mar 22 '19 at 23:10
  • I've gone over the "basic topology" chapter in Rudin, which introduces some elementary concepts from set theory and topology, including metric spaces. Should that be enough? – gtoques Mar 22 '19 at 23:15
  • 1
    Yes! In fact, I started studying topology right after finishing Rudin. It does a decent job motivating some of the ideas of point-set topology, and you can dive deeper from there. – Rushabh Mehta Mar 22 '19 at 23:17
  • 4
    It is good to mention that since topology uses the language of set theory to broaden concepts found in analysis, a good understanding of elementary set theory would be much appreciated. The first chapter in Munkres book "Topology" should give you plenty examples of some usual set operations, which permiate proofs in general topology. – amnesiac Mar 22 '19 at 23:41
  • 1
    A good knowledge of set theory is required –  Jan 31 '21 at 15:56
  • After Rudin you should go through Set Theory & Metric Spaces by Irving Kaplansky. His text can be found online. I bought a hardcover version ‘cause I love his exporatory style so much. If I had profs like him in university,I’d be a professor today. @gtoques –  Aug 29 '21 at 14:23

4 Answers4

12

Much of point-set topology generalizes ideas from real analysis. You'll find continuity restated in terms of open sets so that it can be defined for functions between spaces where a metric doesn't exist (but this generalized definition agrees with analysis' epsilon-delta definition when one does). Likewise, there is a generalized definition for sequence convergence that agrees with analysis in a metric space, but bizarre things can happen outside of one, such as every sequence converging to every point in the space$^\dagger$. You'll also explore specifically which hypotheses we put on a space give rise to different theorems. For instance, in a metric space, we have compactness $\iff$ sequential compactness $\iff$ limit-point compactness. Why is this so? How do these implications change when we remove hypotheses (e.g. when we assume our topological space isn't a metric space, or when we remove the assumption that two points are guaranteed disjoint neighborhoods)? Two theorems you'll recognize from analysis, the Bolzano-Weierstrass theorem and the Heine-Borel theorem, are central to these considerations. So having taken real analysis and encountering things like compactness, continuity, and convergence in a specific kind of topological space (a metric space) makes encountering these concepts in a more general setting easier.

Long story short: real analysis is a sufficient background to get started, and topology is a natural next step.

$^\dagger$ This sort of weirdness made me fall in love with topology. I really can't emphasize this enough—it leads to all sorts of beautiful, often visual constructions.

For instance, here's a connected, locally connected, path-connected, but not locally path-connected subspace of $\mathbb{R}^2$ (source): enter image description here

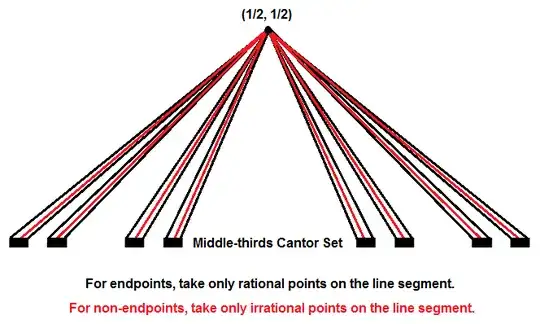
And a choice quotient of this space yields a connected space where removing any point disconnects it into exactly $3$ connected components (source): enter image description here

And here's Cantor's leaky tent: a connected subset of $\mathbb{R}^2$ that becomes totally disconnected(!!) upon removing the single point at the tent's apex. enter image description here

Kaj Hansen
  • 33,511
2

I find that without at least an intermediate knowledge in set theory, it can be hard to delve into more interesting stuff in point-set Topology. Things like Zorn's lemma (AC) are necessary to prove theorems like Tychonoff's.

I highly recommend Munkres Topology - the book is a pleasure to read, introduces topics with plenty of examples, and in a very logical order.

Mariah
  • 3,880
  • But I think a student at the OP's lemma can get comfortable with Zorn's lemma with an hour or two's reading-it's not as if one needs to take a course in set theory. I also might argue that Tychonoff's theorem is the only major result in elementary general topology that relies on choice. – Kevin Carlson Mar 23 '19 at 01:42
  • 1
    @KevinCarlson I think much of point-set topology can be done without choice, but it usually isn't. Moreover, basis set manipulation is absolutely critical to be proficient in, and ordinals provide nice examples. I'm of the opinion that one should learn mathematics slowly, with as thorough a background as possible, especially with something as basic as point-set topology. – Mariah Mar 23 '19 at 01:53
  • I guess my comment was primarily trying to clarify what, exactly, you're trying to claim a student in the OP's situation should do with set theory before moving on to point-set topology. My answer would be "basically nothing", but it sounds like that may not be yours. – Kevin Carlson Mar 23 '19 at 02:03
  • 1
    @KevinCarlson yup, I recommend to learn to some university level set theory before. I may be biased but in my alma mater that is a strongly encouraged prerequisite, and I find it should be so. – Mariah Mar 23 '19 at 02:07
  • I think maybe the book "TOPOLOGY WITHOUT TEARS" by Sidney Morris is a gentle introduction... – Vasile Aug 22 '21 at 15:53
2

In addition to the other answers here, I would strongly recommend you read the book Euler's Gem by D Richeson in your spare time.

I read this in my first or maybe second year as an undergraduate. This is one of the few "popular" maths books that I found nice to read. This book (along with many other things) inspired me to do my PhD in a related area (symplectic topology).

Apart from being a nice read, it gives you a real glimpse of some serious topological theorems, using the geometry of familiar objects such as polyhedra. Remember, you have plenty of time to study the technical side of the subject in the later years of your math degree (I wish someone had told me this when I was an undergraduate). The question of what to study is an important one and you should give it real consideration. I think popular maths texts can be very helpful in this direction.

Nick L
  • 4,520
0

I would start off with learning a good amount of set theory. Charles Pinter: A Book of Set Theory, chapter 1-7 would be a good start.

See here: Book of Set Theory

Then Sets and Metric spaces by Irving Kaplansky.

See here: set Theory and metric spaces

For general topology, a good book which you can cheaply get is Mendelson: Introduction to Topology, 3rd ed. It is heavy on Metric Spaces

See here: https://store.doverpublications.com/0486663523.html

List of chapters

  1. Set theory
  2. Metric spaces
  3. Topological Spaces
  4. Connectedness
  5. Compactness