4

I was given this problem on the codegolf stackexchange, but I don't know where to begin on how to calculate it, except by creating some brute-force program to do it for me (like almost all existing answers currently do).

The problem/challenge has the following requirements:

Input: $n$ and $m$ as dimensions of a grid
Expected output: the amount of unique paths complying to the rules below:

  • All paths start at the origin $[0,0]$
  • You can only travel upwards or towards the right (in increments of 1 step)
  • Paths will wrap-around to the other side (which is the main difference with other similar questions linked below)
  • Only count the paths which end up back at the origin $[0,0]$, without visiting any other coordinates more than once.

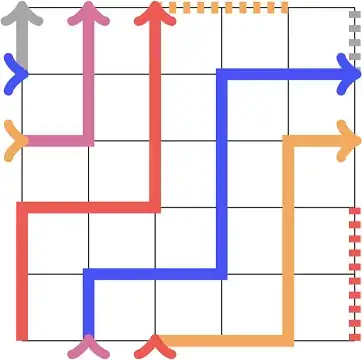
So for $n=m=5$ as input, this would be one of the valid paths:

enter image description here

It starts at the $[0,0]$ origin in the bottom-left and follows the red → orange → pink → blue → grey arrows, ending up back at $[0,0]$ without having visited any other coordinate more than once.

Two other valid paths would be to simply move up five times or move right five times.

Let me start by saying what I do know based on some earlier questions:

To calculate all unique paths for an $n$ by $m$ grid using only the directions up and right, the following formula can be used:

$$a(n,m) = \binom{n+m}{n} = \binom{n+m}{m}$$

i.e. for $n=3, m=4$ the output would be:

$$a(n,m) = \binom{3+4}{3} = \binom{3+4}{4} = 35$$

However, with the requirements and rules above, the expected output for $n=3, m=4$ is supposed to be $66$.

The reason I'm posting this here is because I'm curious if any kind of formula can be found for this problem at all, or if this problem can only be solved reasonably with a brute-force approach?

PS: My math skills aren't that great, so if you use any complex(-looking) mathematical terms and equations, please also ELI5 for me. :)

Kevin Cruijssen
  • 245
  • So arriving at any corner is the same as arriving at $(0,0)$? Are the "dotted" edges forbidden? E.g., would the path $(0,0)$, $(0,2)$, $(5,2)$, $(5,5)$ not be allowed? – Jens Mar 12 '19 at 20:42
  • @Jens I'm not sure why the dotted edges are there tbh. Probably as an indication that they are both at the top and bottom, or left and right side, at the same time. The person who posted the code-golf challenge made that picture. As for your other question: yes, I indeed believe any of the four corners is a valid finishing point, since $(5,5)$ on a 5 by 5 grid, will be $(0,0)$ when modulo-5 is used. The main hard part about this problem are the lines that wrap-around through the sides, and how it can increase the number of possible paths from $(0,0)$ to any of the corners. – Kevin Cruijssen Mar 12 '19 at 22:55
  • Let $T(n,k)$ be the number of paths on the $n\times k$ toroidal grid, where $1\le k\le n$; the proposer of the Code Golf problem has added this sequence to the On-Line Encyclopedia of Integer Sequences as OEIS A324604, giving values up through $k=n=7$. – Brian M. Scott Apr 20 '22 at 21:23

0 Answers0