Do there exist functions $f,g$ in $L^1(\mathbf{R})$ such that the convolution $f \star g$ is (almost everywhere) equal to the indicator function of the interval $[0,1]$ ?
-
isn't f=Dirac delta function and g=indicator function a solution? – Stefan Mar 06 '19 at 18:16
-
5Of course "Dirac delta" is not a function. In particular, does not belong to $L^1(\mathbf{R})$. – GEdgar Mar 06 '19 at 18:20
-
1@GuillaumeAubrun: True (see https://math.stackexchange.com/q/786379/442). But for this question, the two probability measures must be absolutely continuous. – GEdgar Mar 06 '19 at 18:33
-
1The only thing that comes to mind is that if either $f$ or $g$ was bounded (so we consider a convolution of an $L^1$ and an $L^\infty$ function) then $f*g$ would be (uniformly) continuous which obviously doesn't hold here. – Frederik vom Ende Mar 08 '19 at 08:06
-
5Using the Fourier Transform, the question is equivalent to asking whether there exists $\hat{f}, \hat{g}$ such that $$\widehat{f*g} = \hat{f} \cdot \hat{g} = \widehat{\mathbb{1}_{[0,1]}}$$ which is a $\frac{sin(x)}{x}$ function. This seems to be easier to answer. – pitariver Mar 08 '19 at 08:08
-
1This question reminded me of this one on the convolution square root of the Dirac delta. – Giuseppe Negro Mar 09 '19 at 18:10
-
3@GiuseppeNegro: And see here for the (more interesting) multiplication square root of $\delta$: https://mathoverflow.net/questions/235827/square-root-of-dirac-delta-function/235836#235836 – Mar 09 '19 at 21:54
-
1@ChristianRemling: Thank you so much! Yesterday I spent half an hour looking for the question you linked. – Giuseppe Negro Mar 10 '19 at 16:07
-
1This is closely related to the so-called Sonine pairs (see Samko, Cardoso Sonine ... 2003, Kochubei General fractional calculus... 2011). – zhoraster Mar 26 '19 at 10:05
3 Answers
Yes, this works. Let's change the interval to $I=[-1,1]$ for convenience. Then we want to find $f,g\in L^1$ such that $$ \widehat{f}(t)\widehat{g}(t) = \widehat{\chi_I}=\frac{\sin t}{t} . $$ Let's take $\widehat{f}(t) = |t|^{-1/2}$ for $|t|\ge 1$ and then of course $\widehat{g}$ such that $\widehat{f}\widehat{g}=\widehat{\chi_I}$ (so in particular, $\widehat{g}(t)=\textrm{sgn}(t)\,|t|^{-1/2}\sin t$ for $|t|\ge 1$), and then finally, I'm also going to insist that $\widehat{f}, \widehat{g}\in C^{\infty}$.
To show that $f,g\in L^1$, let's first of all discuss the local behavior. This only depends on the large $|t|$ behavior of the Fourier transform, and $|t|^{-1/2}$ has FT $c|x|^{-1/2}$, which is locally integrable (but not locally $L^2$, which is just as well since it's easy to see that at least one of $f,g$ will fail to be in $L^2$ if $f*g=\chi_I$).
The large $x$ asymptotics of $f(x)$ on the other hand depend on the smoothness of $\widehat{f}$, and here we're clearly in great shape since $\widehat{f}''\simeq t^{-5/2}\in L^1$, so $x^2f(x)\in C_0$.
The other function is of the same type, the extra factor $\sin t$ for large $t$ produces essentially a shift in $g$, and $\textrm{sgn}(t)$ amounts to an extra Hilbert transform, which won't affect the local singularities here, so $g\in L^1$ also.
Following the idea of Christian Remling, I have two explicit functions that have the property that $f*g = \mathbf{1}_{[-1,1]}$: \begin{eqnarray} f(x) &=& \frac{K_\frac{1}{4}\left(|x|\right)}{2^{1/4}\pi\Gamma\left(\frac{1}{4}\right)|x|^{1/4}}\\\\ g(x) &=& \frac{\mathrm{sgn}(1-x)}{\sqrt{|1-x|}}\,_1F_2\left(\begin{matrix}-\frac{1}{4} \\ \frac{1}{4}, \frac{3}{4}\end{matrix}; \frac{(1-x)^2}{4}\right) +\frac{\mathrm{sgn}(1+x)}{\sqrt{|1+x|}}\,_1F_2\left(\begin{matrix}-\frac{1}{4} \\ \frac{1}{4}, \frac{3}{4}\end{matrix}; \frac{(1+x)^2}{4}\right)\\ &\,&+ \frac{\Gamma\left(\frac{5}{4}\right)(1-x)}{\sqrt{2}\Gamma\left(\frac{7}{4}\right)}\,_1F_2\left(\begin{matrix}\frac{1}{2} \\ \frac{3}{2}, \frac{7}{4}\end{matrix}; \frac{(1-x)^2}{4}\right)+ \frac{\Gamma\left(\frac{5}{4}\right)(1+x)}{\sqrt{2}\Gamma\left(\frac{7}{4}\right)}\,_1F_2\left(\begin{matrix}\frac{1}{2} \\ \frac{3}{2}, \frac{7}{4}\end{matrix}; \frac{(1+x)^2}{4}\right) \end{eqnarray} Where $K_\frac{1}{4}$ is a modified Bessel function and $\,_1F_2$ is a hypergeometric function. While these aren't the simplest functions, and $g$ is kind of a nightmare, they have the nice property that \begin{eqnarray} \mathcal{F}[f](k) &=& \frac{1}{\sqrt{2\pi}(1+k^2)^{1/4}} \\ \mathcal{F}[g](k) &=& 2\sqrt{2\pi}(1+k^2)^{1/4}\frac{\sin(k)}{k}, \end{eqnarray} so that $f*g = \mathcal{F}^{-1}[\mathcal{F}[f]\cdot\mathcal{F}[g]] = \mathcal{F}^{-1}\left[2\sin(k)/k\right] = \mathbf{1}_{[-1,1]}$.
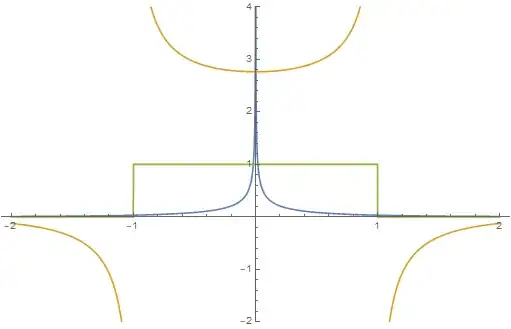
The convolution integral isn't doable analytically, but it can be evaluated numerically. Doing this in Mathematica gives
where the blue is $f$, the yellow is $g$, and the green is $f*g$. Despite their divergences, both $f$ and $g$ are in $L^1$, as the divergences scale as $|x|^{-1/2}$.
- 23,253
By the Cohen–Hewitt factorization theorem, every $f\in L^1(\mathbb R)$ can be written as $g\star h$ for some $g,h\in L^1(\mathbb R).$
- 25,701
- 20
- 52
-
Are you sure? It seems to me that such a $g \star h$ is always a Baire class 1 function (=pointwise limit of continuous functions), but not every $L^1$ function is Baire class 1 even up to a null set (e.g. because such functions have points of continuity). – Guillaume Aubrun Mar 11 '19 at 11:46
-
@GuillaumeAubrun: quite sure. There's no reason for $g\star h$ to be Baire class 1 - the construction of convolution I'm aware of doesn't use continuous functions at all, and any argument using approximation by continuous functions will only use convergence in some metric, not pointwise convergence. – Dap Mar 11 '19 at 23:13
-
If $g \in L^1$ and $h_n \in L^{\infty}$, then $g \star h_n$ is continuous. Now for $h \in L^1$, $g,h \geq 0$, consider a sequence $(h_n)$ in $L^\infty$ such that $h_n \nearrow h$ pointwise. Then $g \star h_n \nearrow g \star h$ pointwise and the latter is Baire class $1$. For a general $g,h$, consider positive and negative parts. Did I miss something here? – Guillaume Aubrun Mar 12 '19 at 09:32
-
By looking at at the references in Cohen & Hewitt papers, I found the following earlier paper by Rudin which proves exactly the result your mentioned : Rudin, W. (1957). Factorization in the group algebra of the real line. Proceedings of the National Academy of Sciences of the United States of America, 43(4), 339. I'm still puzzled since my previous comment seems to contradict that result. – Guillaume Aubrun Mar 12 '19 at 09:48
-
2For completeness, here was the mistake. A general $g \star h$ is the difference of two Baire class 1 functions with values in $[0,+\infty]$, both of which taking the value $+\infty$ on a null set. This does not imply that this difference is a.e. equal to a Baire class 1 function taking values in $\mathbf{R}$. Thanks a lot for the answer! – Guillaume Aubrun Mar 12 '19 at 10:26