13

[I edited the question and put stronger emphasis on "constant curvature" than on "naturalness".]

One of the most prominent problems of ancient mathematics was the squaring of the circle: to construct the square with the same area as a given circle.

A related problem is linearizing the circle: to find a natural transition between a given line segment of length $L$ (having constant curvature $0 = 1/\infty$) and the circle with circumference $U = 2\pi R = L$ (with constant curvature $1/R$) going through circle segments of length $L$ (with intermediate constant curvatures $1/R'$, $\infty > R' > R$).

The question is: Along which paths do the points of the line segment move to finally yield the circle?

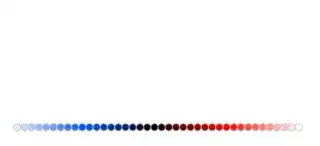
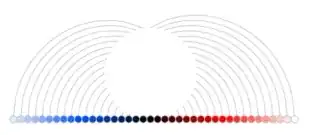
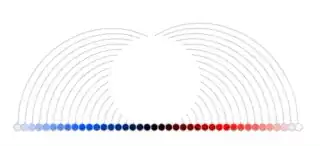
This is how the transition looks like:

enter image description here

The points of the line segments follow these paths:

enter image description here

as can be seen here:

enter image description here

To be honest: Even though these paths look very much like circle segments, I'm not quite sure and I didn't define them by an explicit formula (which I didn't have at hand) but heuristically using some support points and splining.

My questions are:

  • Are these paths really circle segments?

  • If so: How to parametrize them?

  • If not so: What kind of curves are they otherwise?

Please allow me – freely associating – to compare the pictures above with this (artificially symmetrized) picture of The Great Wave off Kanagawa

enter image description here

Hans-Peter Stricker
  • 18,719
  • No, no actual definition, just a definition by example. – Hans-Peter Stricker Feb 27 '19 at 18:00
  • The tags were just chosen to gain attraction: the question has somehow to do with Euclidean geometry, and somehow with projective geometry, and somehow with modular arithmetic. In each case I could explain. – Hans-Peter Stricker Feb 27 '19 at 18:02
  • 5
    I think it would be "natural" to think of a family of curves $\gamma_t$, $t\in[0,1]$, of constant curvature such that $\gamma_0$ is the flat line (curvature 0), $\gamma_1$ is the circle (curvature 1/R) and each $\gamma_t$ has curvature $t\cdot1/R$. – Mars Plastic Feb 27 '19 at 18:06
  • 1
    Just for the composition, +1. – Allawonder Feb 27 '19 at 18:11
  • To the close-voter: What is unclear? I asked very specific questions? What else can I do? – Hans-Peter Stricker Feb 27 '19 at 18:14
  • 2
    Maybe I'm missing something, but this 'transition' seems quite arbitrary to me. – rafa11111 Feb 27 '19 at 18:20
  • @rafa11111: The transition transforms the straight line smoothly and with constant curvature into a circle while preserving distances - as long as the line touches itself - then distance $L$ becomes $0$ and all distances collapse modulo $L$.. So why should this transition be "quite arbitrary"? – Hans-Peter Stricker Feb 27 '19 at 19:29
  • @Allawonder: If you like to "see" more like this: send an email to stricker@syspedia.de. – Hans-Peter Stricker Feb 27 '19 at 19:37
  • I just realized that I misunderstood the question. I thought the OP was interested in which kind of shape is described by the grey area in his animation (given that the curves are indeed circle segments). In my opinion, this is more interesting than speculating about who might find which transition natural. – Mars Plastic Feb 27 '19 at 19:51

2 Answers2

16

What you want can be achieved using circle arcs, centered at $(0,r)$, of radius $r$ and central angle $2\pi R/r$, with $r$ varying between $1$ and $+\infty$. But I don't know if that is "natural" or not. Here's how it looks:

enter image description here

EDIT.

Each endpoint of the arc describes a spiral curve, given by: $$ x={\pi R\over 2\theta}\sin{2\theta},\quad y={\pi R\over 2\theta}\left(1-\cos{2\theta}\right), $$ where $\theta$ is the polar angle. This also gives the simple polar equation: $$ \rho={\pi R}{\sin \theta\over\theta},\quad 0\le\theta\le{\pi\over2}. $$

Intelligenti pauca
  • 55,765
3

If we want this transition to have all the points on the boundary of a circle at all times, then it makes most sense to parameterize by the radius of this circle (and apply a transformation to get it in terms of finite time later). For simplicity, I will also have the transition be to a vertical line.

We shall have the radius of the circle $C_r$ be $r$ and centre be $(-r,0)$, such that $(0,0)$ is on $C_r$ for all $r$. The coordinates of the point at arclength $s$ from $(0,0)$ are then given by $(r (\cos(s/r) - 1), r \sin(s/r))$.

The most natural way to transition would likely be varying the curvature at a constant rate; thus we create a family of curves $f_t:[-\pi, \pi]\to\mathbb{R}^2$ where $t\in[0,1]$ by \begin{align} f_t(s) &= \left(\frac{\cos(s(1-t))-1}{1-t}, \frac{\sin(s(1-t))}{1-t}\right)&t<1\\ f_1(s) &= (0, s)& \end{align}

Since the goals here seem to be rather subjective, I would attempt this and see how it looks to you (beyond making substitutions as needed to result in a horizontal line).

Khoross
  • 91