Is the percentage symbol a constant?

Question

1. Isn't the percentage symbol actually just a constant with the value $0.01$? As in $$ 15\% = 15 \times \% = 15 \times 0.01 = 0.15. $$

2. Isn't every unit actually just a constant? But why do we treat them in such a special way then?

Answer 1

Isn't the percentage symbol actually just a constant with the value $0.01$?

No. If it were, all of the following would be valid constructs:

$$ 30+\%\,50=30.5\\ 90\,\%\,\mathrm{cm}=0.9\,\mathrm{cm}\\ 2-\%=1.99\\ \%^2=0.0001 $$

The percentage symbol is a unit. When converting between units, it's easy to treat them as constants that represent the conversion ratio, and multiply (for example, the $\mathrm{m}$ unit can be thought of as a constant equal to $100\,\mathrm{cm}$, in $2\,\mathrm{m}=2(100\,\mathrm{cm})=200\,\mathrm{cm}$). But that isn't the same as saying they're "just constants", as they represent more than that. A unit is not just a ratio, it's a distance or a weight or an amount of time.

This is less obvious with $\%$ because it's a dimensionless unit, representing something more abstract like "parts of a whole" rather than a physical property like mass or surface area. $1\,\%$ is "one one-hundredth of a thing", measuring an amount of something, anything, often something with its own units. A similarly dimensionless unit is the "degree", where $1^\circ$ is "one three-hundred-sixtieth of the way around". Another one is the "cycle", as in "one $\mathrm{Mhz}$ is one million cycles per second". Things like "wholes", "turns", and "cycles" are more abstract than inches or grams, but when applied they still represent tangible measurements, so they aren't any less powerful when treated as units.

---

I mean, I guess every unit is actually just a constant, but why do we treat them in such a special way then?

What then would you say the "constant" is that is represented by "inch", or "second", or "ounce"? Would these ideas not have clear numeric values if every unit were simply a constant?

Again, a unit is not just a constant, it represents something more. I don't have exact vocabulary for this, but I would say a unit is an "amount" of a "dimension". The dimension can be time, space, energy, mass, etc. To even begin to treat a unit as a constant, we need to consider it in terms of a different unit in the same dimension. For example, the unit "millisecond" amounts to different constants depending on whether we think about it in terms of a second ($0.001$), hour ($2.77778\times10^{-7}$), microsecond ($1000$), etc. This constant is not intrinsic to the units themselves, as it only arises when comparing to other units.

Answer 2

Yes, for calculations you can use $\%=\frac{1}{100}$. Of course what is meant by the symbol is an interpretation as "parts of hundred", i.e. as percentage of a given amount.

Answer 3

There are some exceptions. Take for example $20 + 50\%$. This is often interpreted to be equal to $30$, while $20 + 50 \cdot 0.01 = 20.5$.

There is some discussion about whether $20 + 50\%$ is a valid notation. But sometimes it is used and Google and Wolfram Alpha interpret it as $20\cdot 1.5$.

I'm also thinking about $50\%^2$. I don't think you'll see this notation (and you shouldn't use it), but just as a thought experiment: Is this $0.25$ or $0.005$?

Answer 4

I wouldn't say that $\%$ has a value. You can think of $\%$ as "multiply by $\frac{1}{100}"$ as a sort of postfix in the same way as you can think of the "kilo-" prefix as "multiply by $1000$".

So $$ 5\% = 5\ (\text{multiply by} \ \frac{1}{100})=\frac{5}{100}=0.05 $$ in the same way as $$ 2 \ \text{kilograms}=2 \ (\text{multiply by $1000$})\text{ grams}= 2000 \ \text{grams} $$

I usually teach my students this way and I found it to work just fine.

Answer 5

The percent sign is an abbreviation: just substitute "$\color{red}\%$" by "${}\color{red}{\cdot\frac{1}{100}}$", that's all. So for example: $15\color{red}{\%}=15\color{red}{\cdot\frac{1}{100}}=0.15$. Or the other way round: $1.23=123\color{red}{\cdot\frac{1}{100}}=123\color{red}{\%}$.

Answer 6

Well, it really depends. In Chinese schools, students are told that $100\%=1,40\%=2/5$, so % is a constant. In the UK examination system, it appears that % is treated as a unit. Students are NOT expected to write the above two expressions.

However, it is agreed around the world that you should not write something like "$250\%$ liters of water".

So it is a good idea to think of it as a constant, but not write it as a constant.

Other units like cm, mm, kg are like the basis of a vector space or something or the imaginary unit $i^2=1$. The are NOT even like usual numbers because they cannot be added together.

Answer 7

1. Isn't every unit actually just a constant?

   Every constant is a quantity (whether with or without a unit); thus, Celsius is not a constant.

   Isn't the percentage symbol actually just a constant with the value $0.01$?

   While it may appear that $$\%\;:=\;0.01,$$ this is a false definition since neither $(\%-8)$ nor $\dfrac7\%$ are really meaningful.

   In other words, $\%$ is not a constant.

2. But $\%$ is not a unit either, since it does not specify any physical quantity ($7\%$ is not a physical quantity).

3. I agree with Lehs's answer: $\%$ is a postfix operator in the sense that \begin{align}x\%\:\::=\;\;&x\div100\\=\;\;&x\times0.01.\end{align}

4. While $$100+10\%+30\%$$ is frequently interpreted as equalling $143$ instead of $100.4,$ this is merely an abuse of notation.

5. I'd say that $90\%\,\textrm{cm}$ is an odd-looking intermediate step, like $7\,\textrm{cm}\,\textrm{cm}.$

---

When a quantity's value changes from $a$ to $b,$ its percentage change $$\dfrac{b-a}{|a|}\times100\%$$ means its relative change expressed a percentage. The word ‘percentage’ in the phrase percentage change, unlike the symbol ‘$\%$’, is not a postfix operator.

Answer 8

If you want to think about units or dimensional analysis, then probably it is best to interpret 15% as

$$ 15\% = \frac{\text{$15$ units of X}}{\text{$100$ units of X}} $$

(I would read this as "15 units of X per 100 units of X".) For example, the Wikipedia page on dimensional analysis gives the example of debt-to-GDP ratio. $$ 90\% \text{ debt-to-GDP} = \frac{\text{$90$ dollars of debt}}{\text{per $100$ dollars of GDP}} $$

Here both the top and bottom are dollars. But they are two different dollar measurements. So even though the percentage is a dimensionless quantity (dollars/dollars), keeping the units in mind may be wise. Similarly

$$ 10\% \text{ full} = \frac{\text{$10$ liters of water}}{\text{per $100$ liters of container}} . $$

and so on. (edit) So for example, if you want to do a calculation like "How many liters of water are in a 2-gallon container that is 10% full", you do

$$ \text{$2$ gallons of container} ~ \cdot ~ \frac{\text{$3.78$ liters of container}}{\text{$1$ gallon of container}} ~ \cdot ~ \frac{\text{$10$ liters of water}}{\text{$100$ liters of container}} . $$

Of course you could have also done

$$ \text{$2$ gallons of container} ~ \cdot ~ \frac{\text{$10$ gallons of water}}{\text{$100$ gallons of container}} ~ \cdot ~ \frac{\text{$3.78$ liters of water}}{\text{$1$ gallon of water}} ~ \cdot . $$

Answer 9

I think of $\cdot\%$ as an operation that divides the argument by $100$ and multiplies it with the reference value $u$ representing a whole, i. e. $x\% = x\frac{u}{100}$. As such it is actually underdetermined as the reference is implied in the non-mathematical text and not part of the notation.

For example if I give you a $5\%$ discount, the reference unit is implied to be your total, which could be $200\$$ in this example, in which case $5\%=10\$$ (note the unit!)

One could write $\%^u$ to specify the reference unit, such that in the above example $5\%^{200\$}=10\$$, although that would not be commonly understood.

Answer 10

I don't think it has a universally agreed nature.(Symbol,constant,or Unit, or else?) Even though it might have had a single nature at the moment it was created, after a long time usage by people, with non-mathematicans as the majority, its nature might be different among different people's point of view.

In my opinion, I would regard '%' equivalent to the phrase 'out of 100'. That means 15% is read as '15 out of 100' . However, I am pretty sure someone else will have his own interpretation on '%' which leads no contradiction to mine.

Answer 11

It's often convenient to write $x\%$ for $x/100$. The notation $xy$ is also used for the product of $x$ and $y$ (whether numbers, functions, elements of a group, etc.), and these give the same result if you formally set $\% = 1/100$. On the other hand, it would be bizarre to write "$1/\%$ is divisible by $5$" or "$\% + \sqrt{\%} = 0.11$", etc. There's nothing inherently wrong with abusing notation; I have no problem writing $0$ for the integer $0$, the real number $0$, the zero function, the zero element in a vector space, etc. But there's also nothing particularly noteworthy or profound in doing so.

Answer 12

It's a postfix operator. A function written after the argument, $x\%=x/100$, instead of before the argument as in normal prefix notation $f(x)$ or $\Delta x$.

Answer 13

I believe you can think of it both ways.

It’s a symbol for “parts of a hundred” that happens to have a constant value behind it, and at the same time it’s a constant that happens to have a symbolic meaning behind it.

Answer 14

It is not a constant. It can be thought of as a unit if you like, but is probably best thought of as merely a syntax. A phrasing I find effective is to say that they are different spellings of a number.

The reason it is not a constant is because it cannot be used in all situations where a constant could be used. For example, $100x$ cannot be meaningfully written as $\frac{x}{\%}$. Were $\%$ to be a constant, that would be a reasonable thing to write. It would be as reasonable as writing $\frac{x}{\pi}$.

You can get away with thinking of percents as units. Like with your approach of treating it as a constant, the math tends to work out. However, it doesn't really work well as a unit in general. While the axiomization of units is still an open problem, it is typically not true that $100\ m = 1\ \frac{m}{\%}$ or $1\ m = 100\ m\cdot \%$. This makes it an awkward sort of unit.

I do see "%" used as a unit from time to time, but it's typically shorthand for a particular percentage. I might see a graph of a chemical reaction efficiency written as "%/mol". Indeed, this is using "%" as a unit, but in such a graph it would really be a shorthand for "percent efficiency of the reaction." The same graph might instead be labeled with "%yield/mol" without really changing the meaning any. In this case, I think it is clear that "%" is not really acting as a unit in the way you might be used to. It's really just a letter, no different than "a" or "q."

Instead, perhaps the most reliable way of treating percents is as an alternate spelling for a number when writing it down. This is a nuanced difference: it suggests that 10% and 0.1 are not just equal, they are in fact merely two ways of writing down the same number. This would be no different than how a programmer might write 0x1F to denote the number 31 in a base-16 notation, how a Chinese person might elect to write 三十一 to denote the same number, or how we might write "thirty one." They are merely different ways of writing the same number.

This is a subtle difference, but sometimes it can be helpful. For example, at some point you will come across the proof that 0.9999.... = 1.0. This proof is very disconcerting at first, because you assume 0.9999... and 1.0 are two distinct numbers, so they could never be equal. But when you really dig into the meaning of that funny little "..." symbol, you discover there's a better way to think of it. "0.9999..." and "1.0" are simply two spellings of the same number. One relies on an infinite series to acquire its meaning, while the other does not, but they mean the same number.

Answer 15

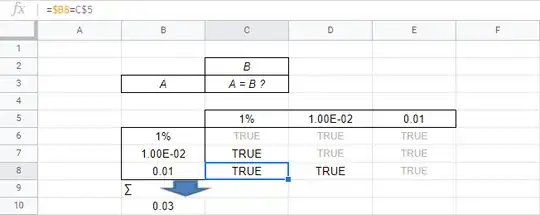
To me, this is just a notation i.e. a way of expressing numbers, e.g.

$0.01 = 1\% =10^{-2} = 1\text{e-}02$

Which would also explain why it is said to be dimensionless.

At least Excel-like apps agree on that matter,