28

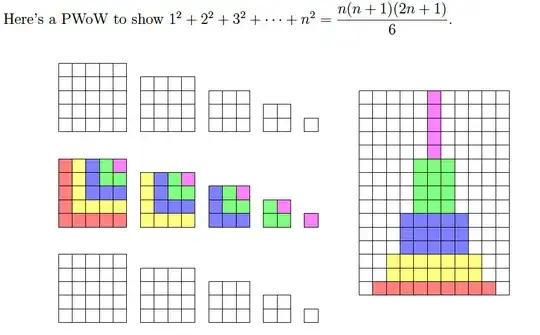
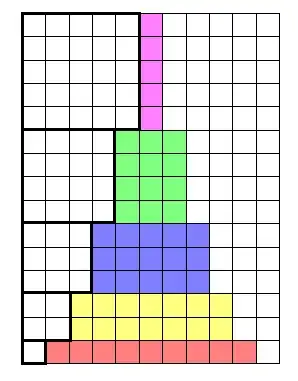
enter image description here

enter image description here

enter image description here

I understand how to derive the formulas for sum of squares, consecutive squares, consecutive cubes, and sum of consecutive odd numbers but I don't understand the visual proofs for them.

For the second and third images, I am completely lost.

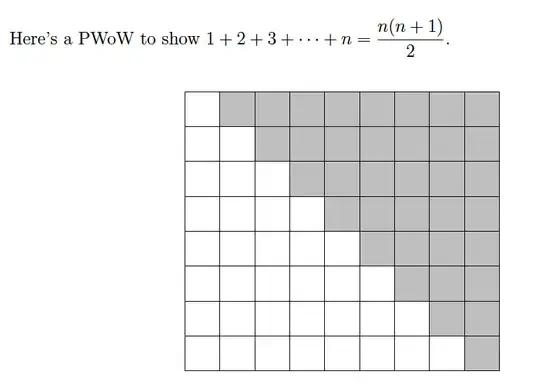
For the first one I can see that there are $(n+1)$ columns and $n$ rows. I'm assuming that the grey are even and that the white are odd or vice versa? So in order to have an even amount of odds and evens you must divide by two?

How can I create an image for the sum of consecutive odd numbers ($1+3+5+...(2n-1)^2 = n^2$)

Blue
  • 83,939
user8358234
  • 402
  • 5
  • 16
  • In the first image, the white squares represent the terms of the sum $1+2+3+\cdot\cdot\cdot+n$. Each square can be assumed to have unit area. The first row has $1$ white square, the second $2$ and so on. The sum is then merely the area of the white portion of the image, which is half the area of the $n\times(n+1)$ rectangle – Shubham Johri Jan 21 '19 at 09:00
  • 1
    I believe the second PWoW finds inspiration in the fact that $n^2$ is the sum of the first $n$ odd natural numbers.$$1^2+2^2+3^2+\cdot\cdot\cdot+n^2=1+(1+3)+(1+3+5)+\cdot\cdot\cdot+(1+3+5+\cdot\cdot\cdot+2n-1)\=n\times1+(n-1)\times3+\cdot\cdot\cdot+2\times(2n-3)+1\times(2n-1)$$ – Shubham Johri Jan 21 '19 at 09:06
  • 1
    The question didn't originally ask for a proof of the sum of consecutive odd numbers. (In general, you shouldn't add to a question once you have gotten answers, but be that as it may ...). That the sum of consecutive odd numbers is a square is actually illustrated with the colorful blocks on the left of the second image: note that the bands of color are the consecutive odd numbers. – Blue Jan 21 '19 at 09:40
  • 1
    @Blue thank you. i will refrain from doing that next time – user8358234 Jan 21 '19 at 09:41
  • @user8358234: Good to know. :) The comment was intended both as (friendly!) advice to you, and as notice to future readers who might wonder why the existing answers don't address the last issue. – Blue Jan 21 '19 at 09:46
  • For sum of squares, there a nice "graphical" "Gaussian-style" proof here. – Hypergeometricx Jan 21 '19 at 14:04

3 Answers3

13

The second picture gives a visual proof for the formula $$3(1^2+2^2+3^2+\dots +n^2)=\frac{n(n+1)}{2}\cdot (2n+1)$$ for $n=5$. The sum of the areas of the $3\cdot 5$ squares on the right $$3(1^2+2^2+3^2+4^2+5^2)$$ is equal to the area of the rectangle on the left with height $1+2+3+4+5=\frac{6\cdot 5}{2}$ (see the first formula) and base $2\cdot 5+1$.

The third picture gives a visual proof for the formula $$4(1^3+2^3+3^3+\dots +n^3)=(n(n+1))^2$$ for $n=6$. Starting from the center and evaluating the areas of each concentric frame, the area of the large square of side $7\cdot 6$ is $$4\cdot 1^2+8\cdot 2^2+12\cdot 3^2+16\cdot 4^2+20\cdot 5^2+24\cdot 6^2\\ =4(1^3+2^3+3^3+4^3+5^3+6^3)$$

Robert Z
  • 147,345
  • for the second picture why is it doing $3(1^2+..._n^2) = \frac{n(n+1)}{2}(2n1)$? First I don't know where this 3 comes from, why it is necessary or if it's just arbitrary and secondly shouldn't the denominator be 6 and not 2? – user8358234 Jan 21 '19 at 09:34
  • In the given picture, on the right side, we have $3$ copies of each square. Of course $3(1^2+2^2+3^2+\dots +n^2)=\frac{n(n+1)}{2}\cdot (2n+1)$ is equivalent to $(1^2+2^2+3^2+\dots +n^2)=\frac{n(n+1)(2n+1)}{6}$. – Robert Z Jan 21 '19 at 09:38
  • ohh got it, sorry that was silly of me. but why are there three copies of the squares? why is it necessary for this proof? – user8358234 Jan 21 '19 at 09:40
  • 1
    The two copies of white squares fill the white part of the rectangle (left and right). The third copies (with colored stripes) fill the central part of the rectangle. – Robert Z Jan 21 '19 at 09:43
  • thank you for such a detailed answer. i have one more question about the third image: if n = 6, then the total amount of squares should be 1764 and that is how many total squares there are in that image right? and why is it that the larger square is 7 x7? why don't we start with a 1 x 1 square and end up with a 6 x 6 square as the largest square? – user8358234 Jan 21 '19 at 09:52
  • also i don't understand this statement: $41^2+ 82^2+12*3^2+...$ I mean I understand what you're doing and how it gets you the next statement but i don't see where in the image it is represented – user8358234 Jan 21 '19 at 09:57
  • In the image you have $4$ square $1\times 1$ at the center, $8$ square $2\times 2$ in the first frame, $12$ square $3\times 3$ in the second frame... – Robert Z Jan 21 '19 at 10:00
11

Sum of naturals

The rectangle has $n$ by $n+1$ cells and contains twice the sum of the numbers from $1$ to $n$. Hence

$$2\,(1+2+\cdots n)=n(n+1).$$

Sum of perfect squares:

The cells from the three sets of squares (of areas $1$ to $n^2$) are rearranged in a rectangle. The height of the rectangle is the sum of integers from $1$ to $n$, while the width is $2n+1$. Hence

$$3\,(1+4+\cdots n^2)=\frac{n(n+1)}2(2n+1).$$

Sum of perfect cubes:

Every ring contains $4k$ squares of area $k^2$, hence in total four times the sum of the $n$ first cubes. At the same time, they form a square of side twice the sum of integers from $1$ to $n$. Hence

$$4\,(1+8+\cdots n^3)=(n(n+1))^2.$$

To make the second picture even more readable:

enter image description here

  • so for the perfect squares, the height and width you are stating for right side of the image right? but why is that the case that it is that based off the left side of the image – user8358234 Jan 21 '19 at 09:43
  • @user8358234: observe how the cells are displaced and see that their number is preserved. –  Jan 21 '19 at 09:44
  • @user8358234 It took me a while to see it; the white areas are made up of 5x5, 4x4, 3x3, 2x2 and 1x1 squares. They should have colors too. – JollyJoker Jan 21 '19 at 13:11
  • @JollyJoker: the white cubes were put on the left side for some reason. When you understand the reason, you have it. –  Jan 21 '19 at 13:46
-2

For a diagram of the sum of consecutive odd nos, use the diagram in your sum of squares that shows a red L shape with an inner yellow L shape, with an inner blue L shape with an inner green L shape with a single green square.

jsc42
  • 1