Goal
I would like to proof than the Negative Log Likelihood Function of Sample drawn from a Normal Distribution is convex.
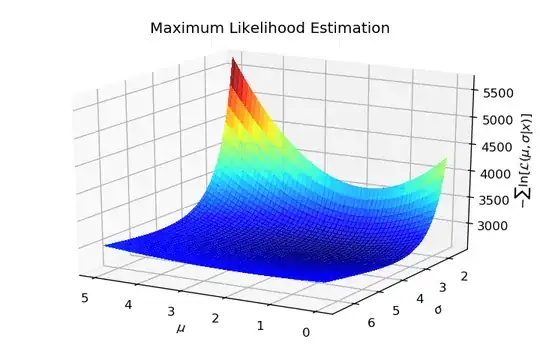
Below a Figure showing an example of such function:
Motivation of this question is detailed at the end of the post.
Sketching the demonstration
What I did so far...
First I have written the likelihood function for a single observation:
$$\mathcal{L} (\mu, \sigma \mid x) = \frac{1}{\sqrt{2\pi\sigma^2} } e^{ -\frac{(x-\mu)^2}{2\sigma^2} }$$
For convenience I take the Negative Logarithm of the Likelihood function, I think it does not change the extremum because Logarithm is a monotonic function:
$$f(\mu, \sigma \mid x) = -\ln \mathcal{L} (\mu, \sigma \mid x) = \frac{1}{2}\ln(2\pi) + \ln(\sigma) +\frac{(x-\mu)^2}{2\sigma^2}$$
Then I can assess the Jacobian (check: 1 and 2):
$$ \mathbf{J}_f = \left[ \begin{matrix} -\frac{x-\mu}{\sigma^2}\\ -\frac{(x-\mu)^2 - \sigma^2}{\sigma^3} \end{matrix} \right] $$
And the Hessian (check 3, 4 and 5):
$$ \mathbf{H} = \left[ \begin{matrix} \frac{1}{\sigma^2} & \frac{2(x - \mu)}{\sigma^3} \\ \frac{2(x - \mu)}{\sigma^3} & \frac{3(x - \mu)^2 - \sigma^2}{\sigma^4} \end{matrix} \right] $$
Of the Negative Log Likelihood function.
Now, I compute the Hessian of the Negative Log Likelihood function for $N$ observations:
$$ \mathbf{A} = \frac{1}{N}\sum\limits_{i=1}^{N}\mathbf{H} = \left[ \begin{matrix} \frac{1}{\sigma^2} & \frac{2(\bar{x} - \mu)}{\sigma^3} \\ \frac{2(\bar{x} - \mu)}{\sigma^3} & \frac{\frac{3}{N}\sum\limits_{i=1}^{N}(x-\mu)^2 - \sigma^2}{\sigma^4} \end{matrix} \right] $$
If everything is right at this point:
- Proving the function is convex is equivalent to prove than the Hessian is semi-positive definite;
Additionally I know that:
- A semi-positive definite Matrix must have all its eigenvalues non-negative;
- Because the Hessian Matrix is symmetric, all eigenvalues are real;
So if I prove than all eigenvalues are positive real numbers, then I can claim the function is convex. We can also check, as @LinAlg suggested, that both determinant and trace of Matrix $\mathbf{A}$ are positive:
$$ \begin{align} \det(\mathbf{A}) \geq 0 \Leftrightarrow & \frac{3}{N}\sum\limits_{i=1}^{N}(x-\mu)^2 - \sigma^2 - 4(\bar{x} - \mu)^2 \geq 0 \\ \operatorname{tr}(\mathbf{A}) \geq 0 \Leftrightarrow & \frac{3}{N}\sum\limits_{i=1}^{N}(x-\mu)^2 \geq 0 \end{align} $$
It is obvious that $\operatorname{tr}(\mathbf{A}) \geq 0$.
Inequality
The inequality $\det(\mathbf{A}) \geq 0$ is not obvious at the first glance, it requires a bit of algebra. Expanding all squares, applying sum, simplifying and grouping gives:
$$ 3\left[\frac{1}{N}\sum\limits_{i=1}^{N}x^2 - \bar{x}^2\right] -(\bar{x}-\mu)^2 -\sigma^2 \geq 0 $$
Now I can rewrite it using Standard Deviation Estimation:
$$ 3\left[\frac{N-1}{N}s^2_x - \sigma^2\right] + 2\sigma^2 \geq (\bar{x}-\mu)^2 $$
For $N$ sufficiently large it tends to:
$$ 3\left(s^2_x - \sigma^2\right) + 2\sigma^2 \geq (\bar{x}-\mu)^2 $$
Or:
$$ \left|\bar{x}-\mu\right| \leq \sqrt{3s^2_x - \sigma^2} $$
Provided the radicand is non -negative. This last inequality provides a bound for Mean Asbolute Error which must be lower than approximately $\sqrt{2}\sigma$. Finally, if the estimators converge to expected values it reduces to:
$$ \sigma \geq 0 $$
Which is trivially true by definition.
My interpretation of this inequality is:
If we have sufficiently large statistics, drawn from a Normal Distribution, and the Mean and Variance Estimation are close enough to their expected value then the Negative Likelihood Function should be convex. If expected values $\mu$ and $\sigma$ are known, it is possible to assess the convexity.
Questions
- Are my reasoning and the interpretation of the result correct?
- Can we formally prove that $\det(\mathbf{A}) \geq 0$?
Motivation
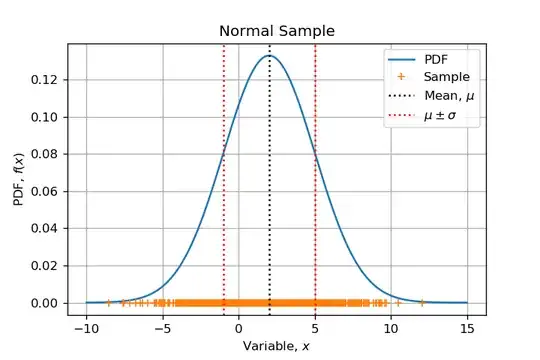
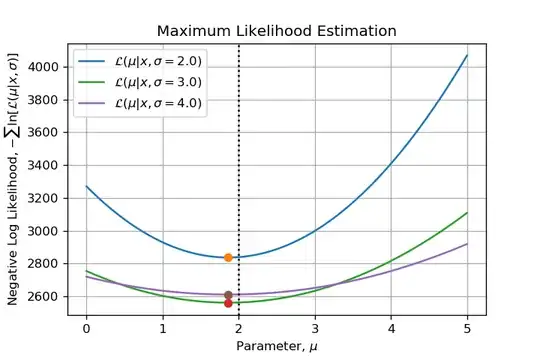
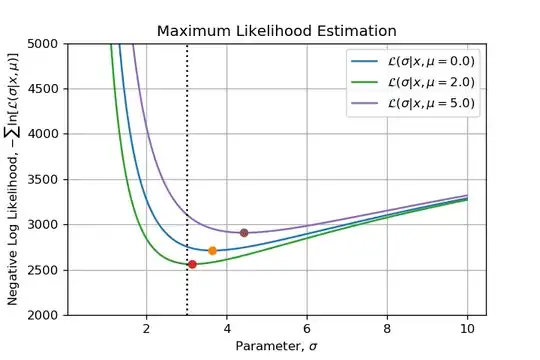
This question arose from a numerical example I develop. I am sampling from a Normal Distribution $\mathcal{N}(\mu=2, \sigma=3)$ with $N=1000$ and I would like to emphasize all steps of a Maximum Likelihood Estimation. Then when I visualized the function to minimize I wondered: Can we say that this function is convex? Which made me write this post on MSE.