After reading some graph theory and talking with experts, I was intrigued. I would like to construct and visualise an infinite planar graph with degree sequence: $$D=(4^4,6^\infty)$$ where the superscripts denote the number of vertices with that degree.
What is the number of graphs with this degree sequence?
Thanks in advance.
There are infinitely many graphs with this degree sequence.
First, here is one possible graph with degree sequence $(6^\infty)$: an infinite triangular lattice.
One way to add four vertices of degree $4$ is to pick two places where we "split up" a degree-$6$ vertex into two adjacent degree-$4$ vertices:
There are other ways to make a graph with degree sequence $(4^4,6^\infty)$, but this operation can already be done in infinitely many non-isomorphic ways, since we can put the two pairs of degree-$4$ vertices arbitrarily far apart in the infinite lattice.
(And there are also other graphs we can start with that have degree sequence $(6^\infty)$, this one is just the nicest.)
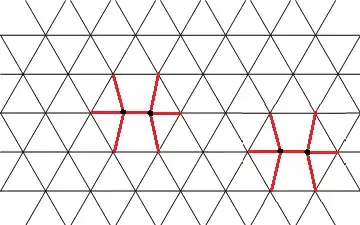
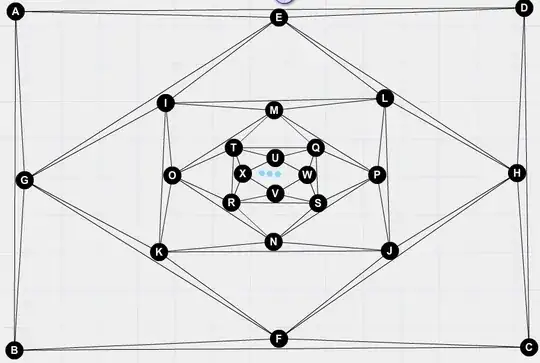
It is easy to construct an infinite tree with any reasonable sequence as its degree sequence. (All ones, for example, would not be reasonable.)
For starters, here is a tree whose degree sequence, in your notation, is $(5^1,6^\infty)$. The vertex set is the set of all finite sequences $\langle x_1,x_2,\dots,x_n\rangle$ (including the null sequence) with $x_i\in\{0,1,2,3,4\}$, and with an edge joining $\langle x_1,x_2,\dots,x_n\rangle$ to $\langle x_1,x_2,\dots,x_n,x_{n+1}\rangle$. The null sequence has degree $5$, the rest have degree $6$.
By imposing the further conditions $x_1\ne0$ and $x_1\in\{1,2,3\}\implies x_2\in\{1,2,3\}$ we get a tree with degree sequence $(4^4,6^\infty)$; the vertices of degree $4$ are the null sequence and the sequences $\langle1\rangle$, $\langle2\rangle$, and $\langle3\rangle$.
The number of trees with degree sequence $(4^4,6^\infty)$ is $\aleph_0$; each such tree is determined up to isomorphism by the smallest (finite) subtree containing all the vertices of degree $4$, those vertices being marked.
If $6^\infty$ means that there are $\aleph_0$ vertices of degree $6$, then there are $2^{\aleph_0}$ isomorphism classes of such graphs.
There can't be more than that, because each graph with $\aleph_0$ vertices can be represented as a subset of $\mathbb N\times\mathbb N$ in at least one way.
On the other hand, we can construct that many different graphs:
Start with an infinite tiling of the plane with equilateral triangles. That gives you an infinity of degree-6 vertices. Now pick two of them and split each of those two into two degree-4 vertices:
\ / \ /
--O-- --> --O--O--
/ \ / \
This gives at least one graph with your degree sequence. But there are uncountably many ways we can modify it to give rise to a non-isomorphic graph. Namely, somewhere in the grid we can slice it open with a cut stretching to infinity:
\ / \ / \ / \ / \ / \ / \ / \ /
--O---O---O---O---O---O---O---O--
/ \ / \ / \ / \ / \ / \ / \ / \
O---O---O---O---O---O---O---O---O
\ / \ / \ /
--O---O---O---O---O---O---O---O--
/ \ / \ / \ / \ / \ / \ / \ / \
O---O---O---O---O---O---O---O---O
\ / \ / \ / \ / \ / \ / \ / \ /
and then fill the gap with another copy of the same sliced-open grid, stitched to your existing grid along the edge. (You'll need to squeeze it to make it fit, of course -- but even if your concept of "infinite planar graph" requires that the set of vertices has no limit points in the plane, you can achieve this by squeezing most of the the new copy out towards infinity such that at every finite distance from the place we're looking at here there's a certain minimal spacing between the vertices).
You can keep making such cuts and filling them in at different spacings. The endpoints of the original cuts will be topologically distinguishable from the rest of the graph, because they will be the only places in the graph there's a cycle of degree-6 vertices of length more than 3 where the shortest path between any two vertices in the cycle is along the cycle. We can encode an arbitrary subset of $\mathbb N$, for example, as the distances between those cut endpoints.
In this graph I started with four vertices in the shape of a square, then kept connecting vertices in the interior to match the desired degree sequence.
