1

I struggle to understand what's the difference between Probability distribution (https://en.wikipedia.org/wiki/Probability_distribution) vs. probability mass function (https://en.wikipedia.org/wiki/Probability_mass_function) or Probability density function (https://en.wikipedia.org/wiki/Probability_density_function). Both probability distribution and lets say PMF seem to reflect probability of values of a random variable. Note that I do not ask the difference between PDF and PMF.

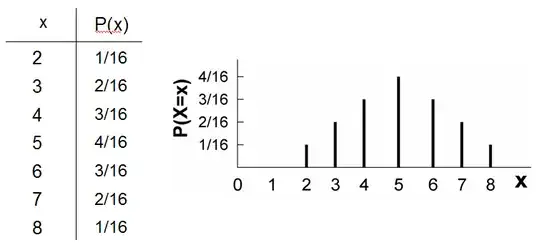
Consider the following example when a 4-sides dice is rolled twice. X is the sum of two throws. I calculate the probability mass function (left) and then show the result graphically (right). But it seems that it is fair to call this graph probability distribution. Isn't it?

Thanks!

enter image description here

John
  • 435
  • 1
    The key is that the Probability Mass Function is associated to discrete random variables, while the Probability Distribution Function is associated to continuous random variables. There are some authors that use this while others simply call it PDF. While the PMF is defined as $P(X=x)$ the PDF could be heuristically defined as $P(x+\epsilon \geq X \geq x-\epsilon)$, since for a continuous r.v. $P(X=x)=0$ – Chaos Dec 03 '18 at 18:45
  • In the context of measure theory a probability distribution is commonly a pushforward-measure induced by a random variable/vector. This is the Kolmogorov-definition and the measure is prescribed by $B\mapsto P(X\in B)$. Using the Kolmogorov-definition we do not have to distinguish between concepts like discrete distributions (linked to a PMF), absolutely continuous distributions (linked to a PDF) or something in between. – drhab Dec 03 '18 at 18:53
  • Thanks, but I am asking not about "Probability Distribution Function", but about "Probability distribution" (https://en.wikipedia.org/wiki/Probability_distribution). Probability distribution can be binomial which is discrete. – John Dec 03 '18 at 18:54
  • My former comment concerns "probability distribution" and the Kolmogorov-definition can be found on the link you provide. – drhab Dec 03 '18 at 18:58
  • My response was for the first answer :) – John Dec 03 '18 at 19:01
  • Put in other way: we have PMF and PDF. Can I say that they are types of probability distributions? – John Dec 03 '18 at 19:05
  • @John My bad, I mixed up concepts. – Chaos Dec 03 '18 at 19:10
  • I would say "no" (but I am not an authority on this). Personally I use the Kolmogorov definition for distribution. Then there are indeed types of probability distributions, but those I label with the terms "discrete" and "absolutely continuous". The discrete probability distribution is characterized by a PMF and the absolutely continuous probability distribution by a PDF.IMV the main thing is here that mathematicians use as much as possible the same terminology. – drhab Dec 03 '18 at 19:11
  • I see, thanks for your help! – John Dec 03 '18 at 19:14
  • 5
    Does this answer your question? Probability density function vs. probability mass function –  Jan 01 '22 at 05:26

2 Answers2

2

"Probability distribution" is a general term describing a mathematical entity that is represented by the "cumulative distribution function" (or just "distribution function") and also by its "probability mass function" or "probability density function" (or just "density"), when it exists.

For example the following sentence is perfectly correct even though a bit wordy: "the cumulative distribution function of the Normal probability distribution is XXX, while its probability density function is YYY".

As to what your graph reflects, the cumulative distribution function is non-decreasing by definition.

Alecos Papadopoulos
  • 10,546
0

Probability density functions are always associated with continuous random variables. Continuous variables, are variables which can be measured, such as time, and length. However, a probability mass function is a function which only takes in discrete values for its random variable. However; in both cases the function must satisfy two conditions in order to be a PDF or PMF: 1) The honesty condition (The sum of all the values or outcomes must equal one for discrete cases, and integral for continuous cases). 2) Given any outcome, x, the function f(x) must be between 0 and 1. A probability distribution is a function which assigns a probability to an outcome.

  • Thank you. In my figure, did I plot: a) probability distribution; b) PMF c)both ? – John Dec 03 '18 at 19:52
  • Here it is written that "PMF p(S) specifies the probability distribution for the sum S of counts from two dice." Will you agree? https://en.wikipedia.org/wiki/Probability_distribution#/media/File:Dice_Distribution_(bar).svg – John Dec 03 '18 at 19:57
  • The second condition must be satisfied by a PMF but not necessarily by a PDF. The values taken by a PDF are not probabilities and can exceed $1$. – drhab Dec 04 '18 at 07:35