This is a complicated problem, but if you're careful it does work out. Firstly, let's write out the equation assuming there is a boundary layer or width $\epsilon^\alpha$ at $x_0$, so let $X=(x-x_0)/\epsilon^\alpha$ and $Y(X)=y(x)$. We get
$$ \epsilon^{1-2\alpha}Y_{XX}-\epsilon^{-\alpha}(\epsilon^\alpha X+x_0)^2Y_X-Y=0,$$
expanding
$$ \epsilon^{1-2\alpha}Y_{XX}-\epsilon^{\alpha}X^2Y_X-2Xx_0Y_X-\epsilon^{-\alpha}x_0^2Y_X-Y=0.$$
Now for dominant balance. If $x_0\neq0$, then we would balance $\epsilon^{1-2\alpha}$ with $\epsilon^{-\alpha}$ (you can check that this is the only dominant balance) to give $\alpha=1$. You can leave $x_0$ unknown and determine that it must be 1, but since you already know that we'll use the fact and write our leading-order inner equation at $x=1$ as
$$Y_{XX}-Y_X=0,$$
with boundary condition $Y(0)=1$ (since $x=1$ corresponds to $X=0$). The solution is $Y(X)=A+Be^X$ where $A+B=1$.
If $x_0=0$ then we have a different balance, with $\alpha=1/2$. Let $\mathsf Y(\chi)=y(x)$ with $\chi=x/\sqrt{\epsilon}$ and the leading-order inner equation at $x=0$ is
$$\mathsf Y_{\chi\chi}-\mathsf Y=0,$$
with $\mathsf Y(0)=1$. The solution is $\mathsf Y=Ce^\chi+De^{-\chi}$, and since our solution must be bounded as we exit the boundary layer, we need $A=0$, and the boundary condition gives $D=1$.
The leading order outer solution is, as you found, $y=ke^{1/x}$. You can say here that $k=0$ since the solution must be bounded as you enter each boundary layer, or do it through asymptotic matching.
To fix the remaining constants $k$ and $A$ (or $B$), we need to match all the parts of the solution. To do this, we need the outer solution to be bounded, so we need $k=0$. Alternatively, consider matching the outer solution to the inner solution at $x=0$,
$$\lim_{\chi\rightarrow\infty}e^{-\chi}=\lim_{x\rightarrow0}ke^{1/x}\Rightarrow0=\lim_{x\rightarrow0}ke^{1/x}\Rightarrow k=0.$$ Then the match between the outer layer and the inner layer at $x=1$ gives
$$\lim{x\rightarrow1}0=\lim{X\rightarrow-\infty}A+Be^X\Rightarrow A=0$$
and hence $B=1$.
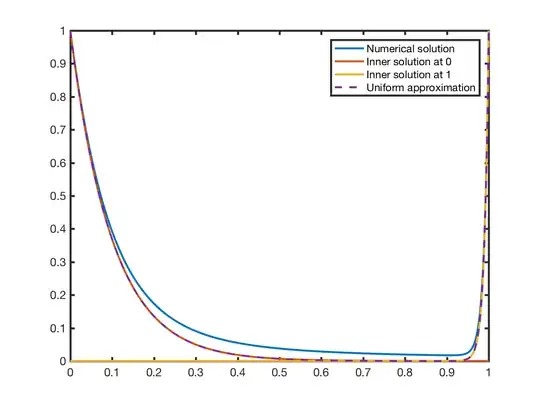
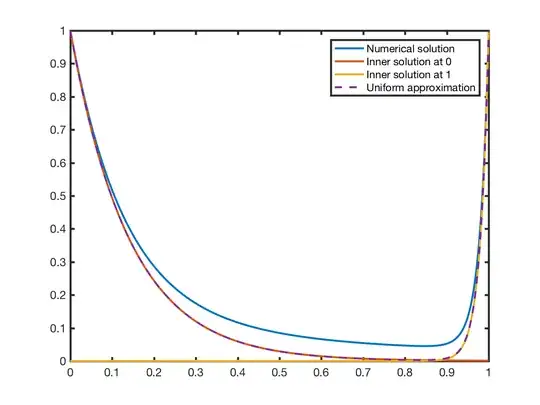
So the inner solution at $x=0$ is $\mathsf Y(\chi)=e^{-\chi}$, the outer solution is $y(x)=0$ and the inner solution at $x=1$ is $Y(X)=e^X$. We can find a uniformly valid approximation by adding the three equations (writing them all in terms of $x$) and subtracting off the matching constants (all zero) as,
$$y_{unif}(x)=e^{x/\sqrt{\epsilon}}+e^{(x-1)/\epsilon}.$$
This will not be particularly accurate, it's an $O(\sqrt{\epsilon})$ approximation, but I did verify that numerically. I've made a plot of the solution for $\epsilon=0.01$ first and $\epsilon=0.02$ second.