He could be asking a trick question. You could draw that figure with your finger on say an iPad, whilst keeping your hand rested the entire tea (but still lifting your finger). If you're drawing it in such a method, then you could do whatever you want with that image. Not just not going over a piece for a second time (by lightning your finger and keeping hand rested once again), but also add extra lines, make it red, delete it entirely. In that case, what your friend said is true - you can draw it without lifting your hand and do whatever you want.
In terms of solving it the proper mathematical way by only using a pen and no tricks like in the above paragraph, then no you cannot. As alluded to in the other answers, the number of nodes (points where several lines intersect) connected to an odd number of lines cannot exceed 2. In this case there are 4 odd-numbered nodes (nodes connected to an odd number of lines), in this case the corners of the inner rectangle. The reason behind this is that to cross every line without lifting your pen, each odd-numbered node must either be started at or ended at (or both). That is not possible if there are more than 2 odd-numbered nodes.
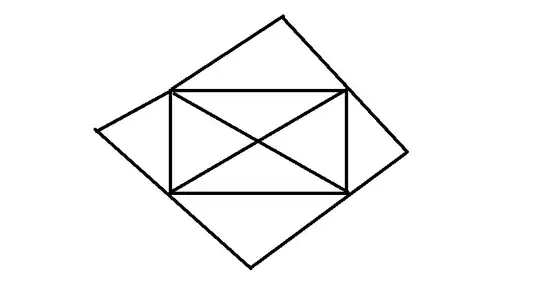 A friend of mine said that if you can draw the figure below without lifting your hand and without going over a piece for a second time, you can do whatever you want. I couldn't do it, no matter how I tried. There's always one piece missing.
A friend of mine said that if you can draw the figure below without lifting your hand and without going over a piece for a second time, you can do whatever you want. I couldn't do it, no matter how I tried. There's always one piece missing.