5

This is a follow-up of this question. In that question, I brought up a theorem I had discovered:

For any complex polynomial $P$ degree $n$:

$$ \sum\limits_{k=0}^{n+1}(-1)^k\binom{n+1}{k}P(a+kb) = 0\quad \forall a,b \in\mathbb{C}$$

In an attempt to generalize it to non-polynomials, I conjecture:

For any function $F:\ \mathbb{R} \rightarrow \mathbb{R}$ that is smooth on $[a, b]$: $$ \lim_{n\to\infty} \sum\limits_{k=0}^{n}(-1)^k\binom{n}{k}F\Big(a+\frac{k(b-a)}{n}\Big) = 0 $$

My rationale for this conjecture is, since any function can be approximated by a polynomial, and the theorem works for all polynomials, taking the limits of the sum of any function to infinity (treat $F$ as an infinite degree polynomial) should result in $0$ as well.

My questions:

If this conjecture is incorrect, can you disprove it? If possible, can you construct a correct version of this theorem (i.e., $F$ has to satisfy some other conditions)?

If this is indeed correct, either a sketch or a hint of a proof is appreciated.

Community
  • 1
  • 1
    A word of caution: a continuous, real-valued function on a compact interval can be approximated uniformly by polynomials (by the Stone-Weierstrass theorem). This does not generalise well to complex-valued functions. – Theo Bendit Oct 30 '18 at 02:59
  • 2
    The statement is true if the $n^{th}$-derivatives of $F$ increases slower than $n^n$. There is a high order version of MVT which asserts for some $c_n \in (a,b)$, we have $$\sum_{k=0}^{n}(-1)^k\binom{n}{k}F\Big(a+\frac{k(b-a)}{n}\Big) = \left(-\frac{b-a}{n}\right)^n F^{(n)}(c_n)$$ I don't think the statement is true in general but I don't have an explicit counterexample. – achille hui Oct 30 '18 at 03:06
  • @Theo I was thinking of Taylor polynomials as approximations of any function. I did not know they don't apply to complex valued functions, do they? Speaking of real, do they work for any smooth functions or just certain ones? –  Oct 30 '18 at 03:16
  • oops, I didn't notice your $F$ can take complex values. The high order version of MVT I quote is for real valued functions. – achille hui Oct 30 '18 at 03:18
  • @achille can I have a reference to the formula you just wrote? –  Oct 30 '18 at 03:20
  • It is a simple application of Rolle's theorem. For a proof, see my answer to an unrelated question. – achille hui Oct 30 '18 at 03:26
  • @Kavi That's funny, because I just checked with my calculator and $(1-e^{1/n})^n$ does seem to tend to $0$ (that is, if your evaluation of the sum is correct). Also, the infinite sum of $e^x$ between $[0,1]$ seems to go to $0$ as well. –  Nov 02 '18 at 14:49

1 Answers1

4

This is not a complete answer.

Please refer also to my answers here and here for details where I show that $$ \frac1{h^n}\Delta_h^n[f](x) = \int_0^{nh} D^n[f](x+t) \sigma_n(t) \,dt $$ where $\sigma_n$ is the probability density function of $S_n=X_1+\dotsb+X_n$ and $X_1,\dotsc,X_n\sim\mathrm{Uniform}(0,h)$ are independent. $\sigma_n$ is a rescaling of the Irwin–Hall distribution (refer to here for a derivation of the PDF).

The expression that you wrote is simply $$ \sum_{k=0}^{n} (-1)^k \binom{n}{k} f\!\left(a+\frac{k(b-a)}{n}\right) = (-1)^n \Delta_{\frac{b-a}n}^n[f](a) = \left(\frac{a-b}n\right)^n \int_a^b f^{(n)}(t) \rho_n(t) \,dt $$ where $\rho_n$ is the PDE of $R_n=\frac{X_1+\dotsb+X_n}n$ and $X_i\sim\mathrm{Uniform}(a,b)$ are independent (related to Bates distribution).

From the characterization of analytic functions, if $f\in C^\infty(\mathbb R)$ is analytic, then $$ \lVert f^{(n)} \rVert_{L^\infty(a,b)} \leq C_{a,b}^n n! $$ Because of the obvious monotonicity of the constant $C_{a,b}$, we can always shrink the interval $(a,b)$ so that $(b-a)C_{a,b}<e$. For such small intervals, we then have $$ \left\lvert\Delta_{\frac{b-a}n}^n[f](a)\right\rvert \leq [(b-a)C_{a,b}]^n n! n^{-n} $$ which converges to $0$ by Stirling's approximation.

This means that your statement is true for analytic functions, as soon as the interval $(a,b)$ is sufficiently short, in the sense that $(b-a)C_{a,b}<e$. In particular, inside each interval there is an interval in which it holds and for each $x\in\mathbb R$ there is an interval containing $x$ for which it holds.

Improvement

Let $f\in C^\infty(\mathbb R)$ be real analytic and $[a,b]\subset\mathbb R$. If the radius of convergence of $f$ in the entire interval $[a,b]$ is larger than some constant $r$, then $C_{a,b}<r^{-1}$. In particular, if $f$ is the restriction of an entire function, then the statement holds true for all segments $[a,b]$. In general, it holds if the singularity of the analytic extension of $f$ closest to the segment is at a distance greater than $|b-a|/e$.

This leads to an idea to find an example of an analytic function $f:\mathbb R\to\mathbb R$ and an interval $[a,b]$ on which the statement does not hold.

New counterexample

Consider $f(z)=\frac1{i-x}$ defined on $\mathbb C\setminus\{i\}$ and take $[a,b]=[-2,2]$. I claim that the statement does not hold. The radius of convergence at $0$ is $1$, which is not greater than $(2+2)/e$, so the above criterion for the validity of the statement is not applicable.

Work in progress

Old incomplete counterexample

I think I have strong evidence that the generalization is false. The idea is to search for a $C^\infty$ function which is badly approximated by polynomials. The first example that comes to mind is $$ f(x) = \begin{cases} 0 & x\leq0 \\ e^{-1/x} & x>0. \end{cases} $$

Working on the interval $[-1,1]$, define $$ a_n = \sum_{k=0}^n (-1)^k \binom{n}{k} f\left(-1+\frac{2k}{n}\right). $$

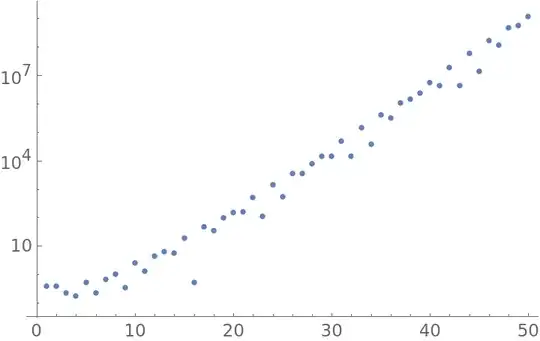
Here is a log-plot of $|a_n|$: enter image description here

This does not seem to converge to $0$...

I will come back to this question if I manage to prove that this sequence really diverges.

Federico
  • 6,010