3

We know of conditions under which we can interchange summation and integration (1, 2).

What are some simple examples where we cannot do so and which we could present to high-school/introductory calculus students (so as to warn them against always simply assuming that we can do so)?

  • You could take any sequence of functions $g_n$ which converges to $g$ and such that $\lim_{n\to\infty}\int g_n\ne \int g$, and consider the series $g_0+\sum_{k=1}^\infty f_k$ with $f_k=g_k-g_{k-1}$. –  Oct 17 '18 at 00:27
  • 1
    @SaucyO'Path, now we only have to provide an example of such a sequence ;) – Yuriy S Oct 17 '18 at 08:58

1 Answers1

2

Let $f_n(x)$ be the triangle function of height $1$ and width $2$, centred on $x=n$. This is what $f_6$ looks like:

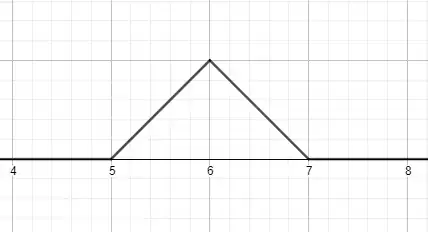
enter image description here

Then

  • $\int_{-\infty}^\infty f_n(x)\,dx=1$ for all $n$
  • $\lim_{n\rightarrow\infty}f_n(x)=0$ for all $x$

So $$0=\int_{-\infty}^\infty \lim_{n\rightarrow\infty}f_n(x)\,dx\ne \lim_{n\rightarrow\infty}\int_{-\infty}^\infty f_n(x)\,dx=1$$

Edited to add: I see now that you asked for a series, not a sequence. So replace the sequence $(f_n)$ in the above with the series $\sum g_n$, defined by $g_1=f_1$ and $g_{n+1}=f_{n+1}-f_n$. Now $\sum_{r=1}^n g_r=f_n$.

TonyK
  • 68,059