17

Given this configuration :

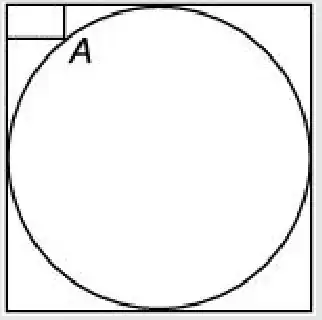
enter image description here

We're given that the rectangle is of the dimensions 20 cm by 10 cm, and we have to find the radius of the circle.

If we somehow know the distance between the circle and the corner of the square then we can easily find the radius. (It's equal to $ \sqrt{2}\times R-R$)

I really can't understand how to solve it. Any help appreciated.

Community
  • 1
Mooncrater
  • 531
  • 1
    This is fascinating, provided it is written correctly. At first it seems there is not enough information, but at the moment, I feel confident that there is. I will mess around with this. – The Count Sep 13 '18 at 18:29
  • 2
    The information you have is $R(1-\cos\alpha) = 2a$ and $R(1-\sin\alpha) = a$, where $a = 10$. From there it follows that $R^2 = (R-2a)^2+(R-a)^2$. – amsmath Sep 13 '18 at 18:29
  • 1
    @amsmath juuuusssssttt beat me to it. Nice! – The Count Sep 13 '18 at 18:31
  • 1
    If you set the upper left corner to be the origin $O(0,0)$, then the center of this circle has coordinates $(R,-R)$, so the circle is given by the equation $(x-R)^2+(y+R)^2=R^2$. Now note that the circle contains the point $(20,-10)$, and calculate $R$ from this. – SMM Sep 13 '18 at 18:31
  • @SMM I deleted my comment because I saw that you had another approach (which I actually like more). – amsmath Sep 13 '18 at 18:40
  • 1
    This question could benefit from adding the 20 cm and 10 cm to the image itself. – NotThatGuy Sep 14 '18 at 13:23

5 Answers5

22

It is just using the pythagorean theorem:
$a=10$ $cm$
$b=20$ $cm$
$(r-a)^2+(r-b)^2=r^2$
$(r-10)^2+(r-20)^2=r^2$
$r^2+100-20r+r^2+400-40r=r^2$
$r^2-60r+500=0$
$r=50$ $cm$
$r=10$ $cm$
The $r=50$ $cm$ is the acceptable answer.

enter image description here

Seyed
  • 9,041
  • 3
    It's worth mentioning that with a slightly looser set of conditions on the question, r=10cm is a valid answer which corresponds to the rectangle occupying the entire top half of a 20x20 square. – Philip C Sep 14 '18 at 07:12
  • @PhilipC, in that case how a circle with r=10cm can touch all four sides of a 20x20 square? – Seyed Sep 14 '18 at 10:12
  • A circle of radius 10cm has a diameter of 20cm, i.e. is 20cm wide and 20cm high, the same as the square. – Philip C Sep 14 '18 at 11:24
  • @PhilipC, yes but how is it going to touch the lower right corner of the rectangle externally? – Seyed Sep 14 '18 at 11:40
  • @XanderHenderson, Is it better now? – Seyed Sep 14 '18 at 12:19
  • That's the slight loosening of the conditions - allowing the circle and rectangle to overlap. – Philip C Sep 14 '18 at 13:00
  • It's also worth noting that under the loosened conditions, the rectangle corresponding to the top half of the square is a special case that happens to fit the particular $a$ and $b$ values of the problem. More generally, this is a solution that allows for the rectangle's diagonal to cut across the circle, starting somewhere outside and ending at the far edge, and the loosening of the conditions is exactly to allow that kind of solution. – John Bollinger Sep 14 '18 at 14:41
4

Place the center of the cricle at $O.$

Let the radius be $R$

The corner of the square is $(R,R)$ I have made a small alteration to the picture to create fewer negative numbers.

Offsetting by the rectange, the corer of the rectangle is $(R-20, R-10)$

And the distance from this point equals the $R.$

That should put you on your way to the solution.

Doug M
  • 58,694
4

The point where rectangle touches the circle is $|R-a|$ and $|R-b|$ away from $x$ and $y$ axes, where $a$ and $b$ are lengths of sides of the rectangle and $R$ is the radius of the circle.

This leads to the equation $$(R-a)^2 + (R-b)^2 = R^2,$$ which has solutions $$R_{1,2} = a+b\pm\sqrt{2ab}.$$

One solution corresponds to a bigger rectangle (compared to the circle), one touching the circle on the other side, which is not the case here. Smaller rectangle compared to the circle means that the circle is bigger if the rectangle is kept fixed, so the correct radius is $$R = a+b+\sqrt{2ab}.$$

Plugging in $a=10$ and $b=20$ gives $R=50$.

Danijel
  • 1,668
3

$(x, y) = (R-20, R-10)$ as a point on the circle $y = \sqrt{R^2 - x^2}$

$R - 10 = \sqrt{R^2 - (R-20)^2}$

$(R- 10)^2 = R^2 - (R-20)^2$

$R^2 - 20R + 100 = R^2 - (R^2 - 40R + 400)$

$R^2 - 60R + 500 = 0$

$(R - 50)(R-10) = 0$

$R = 50$ is the only sensible option.

Phil H
  • 5,689
  • $R=10$ is also possible : the 20x10 rectangle covers the top half of a 20x20 square. – Eric Duminil Sep 14 '18 at 08:10
  • @EricDuminil: But that's not what the diagram shows... The rectangle is clearly entirely outside the circle which it would not be if it covered the entire top half of the square... – Chris Sep 14 '18 at 08:55
  • @Chris It fits with the title : Radius of a circle touching a rectangle both of which are inside a square and I tend to interpret a drawing as a guideline, not a perfect representation on which you could simply measure the solution. I guess it's a personal preference though. – Eric Duminil Sep 14 '18 at 09:01
  • @Eric Duminil and Chris. Thanks for your comments. If you allow a solution of R = 10, which touches 2 corners and a side and intersects the rectangle, there are an infinity of solutions with similar characteristics. Example: a 40x40 square with a radius of R = 20 which doesn't contradict the title. – Phil H Sep 14 '18 at 13:12
  • But if you assume that the circle is inscribed in the square, there are only 2 possibilities at most, right? – Eric Duminil Sep 14 '18 at 13:50
  • The circle R = 20 is inscribed in the 40x40 square and touches the 10x20 rectangle at its top right corner albeit intersecting the rectangle. I prefer the solution that just touches the rectangle without intersecting it. The diagram also defines the point of contact as A. – Phil H Sep 14 '18 at 16:52
1

You can use trig to get the same answer as those above.

Draw three lines: One from the center of the circle to the corner shared by the square and the rectangle. Then draw a line from the center of the circle to the corner nearest to the center of the circle. Draw a final line being the diagonal connecting the previously mentioned corners.

We know the length of the third line by the pythagorean theorem. If we call the side length of the square L, the length of the shorter of the two remaining lines is L/2. The length of the longer, L/sqrt(2).

Find the angle that the diagonal makes with the longer of the drawn lines allows you to apply the cosine rule.

The longer line meets the square's corner at a 45 degree angle with respect to either side. Then angle the diagonal makes with the left side of the square has a tangent of 2.

Apply the cosine rule then solve the resulting quadratic and you get two possible answers, only one of which is plausible.

TurlocTheRed
  • 6,458