Find angle UFO in the picture attached

Question

I sent this problem to Presh Talwalkar who suggested me to send it to this site. I tried many things but was not able to find the correct solution.

1. I made various segments trying to get an equilateral triangle similar to the Russian triangle problem, but no success.

2. I also tried to flip the triangle UFO over side NO but again no success.

3. I tried to find like triangles, but not enough. Could you please give me a hint?

Thanks, R. de Souza

Answer 1

Consider a regular 36-gon $A_1A_2\ldots A_{36}$ inscribed in a circle of radius $R$. Inscribed angle over any side is $5^\circ$. We can see our configuration as it is shown on the picture.

It suffices to prove that $UF$ is parallel to the diagonal $A_{13}A_{34}=EA_{34}$; then we have $\angle NFU=\angle NEA_{34}=25^\circ$, so $\angle UFO= \angle NFO-\angle NFU=100^\circ-25^\circ=75^\circ$.

To prove $UF\parallel A_{34}E$, it is enough to prove $\frac{NU}{UT}=\frac{NF}{FE}$ ($T$ is as on the picture). For we can use the following two formulae:

1. The length of a chord of a circle with inscribed angle $\alpha$ is $2R\sin\alpha$.

2. If $E$ is on a side $BC$ of a $\triangle ABC$, then $\frac{BE}{EC}= \frac{AB\sin\angle BAE}{AC\sin\angle CAE}$.

Now, from $\triangle OEN$ we have: $$\frac{NF}{FE}= \frac{ON\sin\angle NOF}{OE\sin\angle EOF}=\frac{2R\sin 40^\circ\sin 20^\circ}{2R\sin 60^\circ\sin 60^\circ}.$$ From $\triangle NET$ we have: $$\frac{NU}{UT}= \frac{EN\sin\angle NEU}{ET\sin\angle TEU}= \frac{2R\sin 80^\circ\sin 5^\circ}{ET\sin 20^\circ}.$$ By the law of sines on $\triangle NET$, $\frac{ET}{NE}=\frac{\sin 60^\circ}{\sin 95^\circ}$, so $ET= NE\ \frac{\sin 60^\circ}{\sin 95^\circ}= 2R\sin 80^\circ\frac{\sin 60^\circ}{\sin 95^\circ}$ and thus $$\frac{NU}{UT}= \frac{2R\sin 80^\circ\sin 5^\circ}{2R\sin 80^\circ\frac{\sin 60^\circ}{\sin 95^\circ}\sin 20^\circ}= \frac{2R\sin 95^\circ\sin 5^\circ}{2R\sin 60^\circ\sin 20^\circ}.$$

So, for $\frac{NU}{UT}=\frac{NF}{FE}$ it is enough to check: $\sin 40^\circ\sin 20^\circ\sin 20^\circ= \sin 95^\circ\sin 5^\circ\sin 60^\circ$.

We have: $$\sin 95^\circ\sin 5^\circ\sin 60^\circ=\frac{1}{2}(\cos 90^\circ-\cos 100^\circ)\sin 60^\circ= \frac{1}{2}\cos 80^\circ\sin 60^\circ= \frac{1}{4}(\sin 140^\circ-\sin 20^\circ)= \frac{1}{4}(\sin 40^\circ-\sin 20^\circ),$$ and: $$\sin 40^\circ\sin 20^\circ\sin 20^\circ=\frac{1}{2}(\cos 20^\circ-\cos 60^\circ)\sin 20^\circ= \frac{1}{2}(\cos 20^\circ\sin 20^\circ-\frac{1}{2}\sin 20^\circ)= \frac{1}{2}(\frac{1}{2}\sin 40^\circ-\frac{1}{2}\sin 20^\circ)= \frac{1}{4}(\sin 40^\circ-\sin 20^\circ).$$

Answer 2

Without loss of generality, let $OE=1$. By the Law of Sines on the triangle $ONE$, $ON=\dfrac{\sin(40^\circ)}{\sin(60^\circ)}$. Thus, using the Law of Sines on the triangle $ONF$, we get $$NF=ON\,\left(\frac{\sin(20^\circ)}{\sin(100^\circ)}\right)=ON\,\left(\frac{\sin(20^\circ)}{\sin(80^\circ)}\right)=\frac{\sin(20^\circ)\,\sin(40^\circ)}{\sin(60^\circ)\,\sin(80^\circ)}\,.$$ Furthermore, the Law of Sines on the triangle $OUE$ gives $$OU=\frac{\sin(35^\circ)}{\sin(65^\circ)}\,.$$ We also have $NE=\dfrac{\sin(80^\circ)}{\sin(60^\circ)}$ (applying the Law of Sines on the triangle $ONE$), which gives $$NU=NE\,\left(\frac{\sin(5^\circ)}{\sin(115^\circ)}\right)=NE\,\left(\frac{\sin(5^\circ)}{\sin(65^\circ)}\right)=\frac{\sin(80^\circ)\,\sin(5^\circ)}{\sin(60^\circ)\,\sin(65^\circ)}\,,$$ using the Law of Sines on the triangle $UNE$.

Thus, $$\frac{NU}{NF}=\frac{\sin^2(80^\circ)\,\sin(5^\circ)}{\sin(20^\circ)\,\sin(40^\circ)\,\sin(65^\circ)}\,.\tag{*}$$ Note that $$\sin(65^\circ)\,\sin(25^\circ)=\frac{1}{2}\,\big(\cos(40^\circ)-\cos(90^\circ)\big)=\frac{\cos(40^\circ)}{2}\,,$$ where we use the identity $\sin(x)\,\sin(y)=\dfrac{1}{2}\,\big(\cos(x-y)-\cos(x+y)\big)$. Thus, (*) becomes $$\frac{NU}{NF}=\frac{2\,\sin^2(80^\circ)\,\sin(5^\circ)\,\sin(25^\circ)}{\sin(20^\circ)\,\sin(40^\circ)\,\cos(40^\circ)}\,.$$ From the identity $\sin(2x)=2\,\sin(x)\,\cos(x)$, we get $$\frac{NU}{NF}=\frac{4\,\sin(80^\circ)\,\sin(5^\circ)\,\sin(25^\circ)}{\sin(20^\circ)}=\frac{4\,\cos(10^\circ)\,\sin(5^\circ)\,\sin(25^\circ)}{\sin(20^\circ)}\,.$$ That is, $$\frac{NU}{NF}=\frac{4\,\cos(10^\circ)\,\cos(5^\circ)\,\sin(5^\circ)\,\sin(25^\circ)}{\sin(20^\circ)\,\cos(5^\circ)}\,.$$ As $\sin(4x)=2\,\sin(2x)\,\cos(2x)=4\,\sin(x)\,\cos(x)\,\cos(2x)$, we get $$\frac{NU}{NF}=\frac{\sin(25^\circ)}{\cos(5^\circ)}=\frac{\sin(25^\circ)}{\sin(95^\circ)}\,.$$ Ergo, if $\theta:=\angle UFN$, then we have from the Law of Sines on the triangle $UNF$ that $$\frac{\sin(\theta)}{\sin(120^\circ-\theta)}=\frac{NU}{NF}=\frac{\sin(25^\circ)}{\sin(120^\circ-25^\circ)}\,.$$ It follows immediately from the identity $\sin(x)\,\sin(y)=\dfrac{1}{2}\,\big(\cos(x-y)-\cos(x+y)\big)$ that $$\cos(120^\circ+25^\circ-\theta)=\cos(120^\circ-25^\circ+\theta)\,.$$ That is, $$25^\circ-\theta=n\cdot 180^\circ$$ for some integer $n$. As $0^\circ<\theta<100^\circ$ (because $\angle OFN=100^\circ$), we have $n=0$, whence $\theta=25^\circ$. That is, $$\angle UFO=180^\circ-25^\circ-80^\circ=75^\circ\,.$$

Answer 3

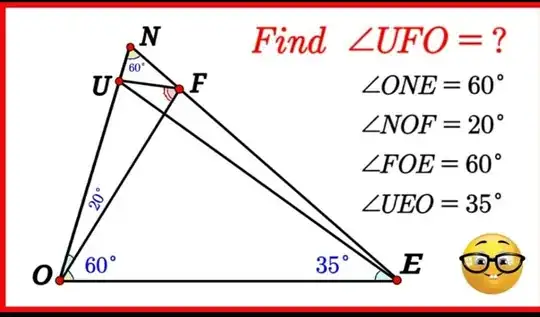
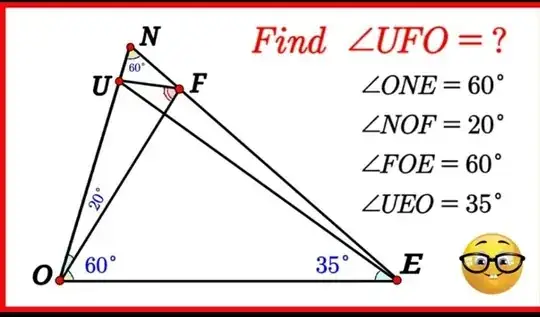
The angles alone do not suffice. We can find out all except $\angle UFO$, $\angle NFU$, $\angle EUF$, or $\angle FUN$; and although we know that $\angle UFO + \angle NFU = 100°$ and $\angle EUF + \angle FUN = 115°$, they are not sufficient. (Even the quadrilateral $UFEO$ does not help, since it just repeats what you find from $\triangle UFO$.)

I think the trick might be to add point $G$ between $O$ and $U$ such that $\overline{GE} \parallel \overline{UF}$. If we call the point where $\overline{OF}$ and $\overline{UE}$ intersect $X$, and the point where $\overline{OF}$ and $\overline{GE}$ intersect $Y$, triangles $\triangle UFX$ and $\triangle OGY$ are similar: $$\begin{aligned} \angle FUX &= \angle GOY = \angle NOF = 20° \\ \angle FXU &= \angle OXE = 180° - 60° - 35° = 85° \\ \angle UFO &= 180° - \angle FUX - \angle FXU = 75° \\ \end{aligned}$$

---

Without any loss of generality, we can choose a Cartesian coordinate system where $O$ is at origin, $F$ is on the positive $y$ axis at $(0, 1)$, and $E$ is at $(E_x , E_y)$ with $E_x \gt 0$.

Because the angles in $\triangle NEO$ sum to $180°$, $\angle ONE = 60°$, and $\angle EON = 60° + 20° = 80°$, we know that $\angle NEO = 180° - 60° - 80° = 40°$. Because $\angle UEO = 35°$, $\angle NEU = 40° - 35° = 5°$.

Similarly, using $\triangle FOE$, we know that $\angle OFE = 80°$.

The slope of $OE$ is $30°$ (because $\angle FOE = 60°$), and the slope of $FE = -10°$ (because $\angle OFE = 80°$). This allows us to find the location of $E$: $$\begin{aligned} y_{OE}(x) &= x \tan(30°) \\ y_{FE}(x) &= 1 - x \tan(10°) \\ y_{OE}(x) &= y_{FE}(x) \end{aligned} \quad \iff \quad x = \frac{1}{\tan\left(\frac{\pi}{18}\right) + \sqrt{\frac{1}{3}}}$$ Substituting into $y_{OE}(x)$ or $y_{FE}(x)$ we get the $y$ coordinate. Thus, $$\left\lbrace\begin{aligned} E_x &= \frac{1}{\tan\left(\frac{\pi}{18}\right) + \sqrt{\frac{1}{3}}} \approx 1.326827896 \\ E_y &= \frac{1}{\sqrt{3}\tan\left(\frac{\pi}{18}\right) + 1} \approx 0.766044443 \\ \end{aligned}\right.$$

The slope of $OU$ is $70°$ (because $\angle NOF = 20°$), and the slope of $EU$ is $5°$ (because $\angle UEO = 35°$, $5°$ more than the slope of $OE$). Using these, we can solve the location of $U = (U_x , U_y)$ (noting that $U_x \lt 0$): $$\begin{aligned} y_{EU}(x) &= E_y + (E_x - x)\tan(5°) \\ y_{OU}(x) &= -x \tan(70°) \\ y_{EU}(x) &= y_{OU}(x) \end{aligned}$$ i.e. $$\left\lbrace\begin{aligned} U_x &= \frac{E_y + E_x \tan\left(\frac{\pi}{36}\right)}{\tan\left(\frac{\pi}{36}\right) - \tan\left(\frac{7\pi}{18}\right)} \approx -0.33162803 \\ U_y &= -\tan\left(\frac{7\pi}{18}\right) U_x \approx 0.91114054 \\ \end{aligned}\right.$$ The $\angle UFO$ fulfills $$\tan\left(\angle UFO\right) = \frac{-U_x}{1 - U_y} \quad \iff \quad \angle UFO = \arctan\left(\frac{U_x}{U_y - 1}\right)$$ which plugging in to a symbolic calculator (I used Maple) does not simplify to anything simple, but numerically yields $$\angle UFO = 75.000000°$$

Using $\triangle FON$, we know $\angle NFO = 100°$. Since $\angle UFO = 75°$, $\angle NFU = 25°$. Because the slope of the line $EU$ is $5°$ and $OF$ is vertical, we know $\angle UXF = \angle OXE = 85°$, and $\angle OXU = \angle FXE = 95°$. Using $\triangle NEU$, we know $\angle EUN = 115°$. Using $\triangle XUF$, we know $\angle XUF = 180° - 75° - 85° = 20°$.

In other words, the angles in the $\triangle XUF$ are $85°$, $20°$, and $75°$, respectively, so there are no similar triangles in the figure we could have used.

Furthermore, while the angle between $x$ axis and line $OE$ is $30°$, the angle between $x$ axis and line $UF$ is $5° + 20° = 25°$, so those two lines are not parallel, either.

I suspect this was one of those puzzles that try to trick you, XKCD style, while the correct answer requires just some work and care for detail; no shortcuts.

---

Here's how saulspatz' answer implements the calculation.

Without loss of generality, choose a Cartesian coordinate system where $O$ is at origin, and $E$ is at $(1,0)$. All the other points have a positive $y$ coordinate.

Two lines intersecting above the $x$ axis, one through $O$ with angle $\phi_1$ to the $x$ axis, and the other through $E$ with angle $\phi_2$ to the $x$ axis, intersect at $(x, y)$: $$\left\lbrace\begin{aligned} y_1(x) &= x \tan(\phi_1) \\ y_2(x) &= (1 - x) \tan(\phi_2) \\ y_1(x) &= y_2(x) \\ \end{aligned}\right. \quad \implies \quad \left\lbrace\begin{aligned} x &= \frac{\tan(\phi_2)}{\tan(\phi_1) + \tan(\phi_2)} \\ y &= \frac{\tan(\phi_1)\tan(\phi_2)}{\tan(\phi_1) + \tan(\phi_2)} \\ \end{aligned}\right. \tag{1}\label{NA1}$$

We can use $\eqref{NA1}$ to find both $U$ and $F$. For $U$, $\phi_1 = 80° = \frac{4}{9}\pi$ and $\phi_2 = 35° = \frac{7}{36}\pi$. Thus, $$\left\lbrace\begin{aligned} U_x &= \frac{\tan\left(\frac{7\pi}{36}\right)}{\tan\left(\frac{4\pi}{9}\right) + \tan\left(\frac{7\pi}{36}\right)} \approx 0.109897 \\ U_y &= \frac{\tan\left(\frac{4\pi}{9}\right) \tan\left(\frac{7\pi}{36}\right)}{\tan\left(\frac{4\pi}{9}\right) + \tan\left(\frac{7\pi}{36}\right)} \approx 0.623257 \\ \end{aligned}\right.$$ For $F$, $\phi_1 = 60° = \frac{1}{3}\pi$ and $\phi_2 = 40° = \frac{2}{9}\pi$ (because $\angle NEO = 180°-60°-20°-60° = 40°$): $$\left\lbrace\begin{aligned} F_x &= \frac{\tan\left(\frac{2\pi}{9}\right)}{\tan\left(\frac{\pi}{3}\right) + \tan\left(\frac{2\pi}{9}\right)} \\ F_y &= \frac{\tan\left(\frac{\pi}{3}\right) \tan\left(\frac{2\pi}{9}\right)}{\tan\left(\frac{\pi}{3}\right) + \tan\left(\frac{2\pi}{9}\right)} \\ \end{aligned}\right.$$

Next, we can use basic vector algebra, $$\cos\left(\angle XYZ\right) = \frac{\overline{XY} \cdot \overline{ZY}}{\left\lVert\overline{XY}\right\rVert \left\lVert\overline{ZY}\right\rVert} = \frac{\overline{XY} \cdot \overline{ZY}}{\sqrt{\left(\overline{XY}\cdot\overline{XY}\right)\left(\overline{ZY}\cdot\overline{ZY}\right)}}$$ To solve the angle $\angle UFO$, we need vectors $\overline{UF}$ and $\overline{OF}$: $$\left\lbrace\begin{aligned} \overline{UF} &= \left [ \begin{matrix} F_x - U_x \\ F_y - U_y \end{matrix} \right ] \\ \overline{OF} &= \left [ \begin{matrix} F_x \\ F_y \end{matrix} \right ] \\ \end{aligned}\right.$$ This means the solution is $$\angle UFO = \arccos\left( \frac{F_x (F_x - U_x) + F_y (F_y - U_y)}{\sqrt{\left( F_x^2 + F_y^2 \right)\left((F_x - U_x)^2 + (F_y - U_y)^2\right)}}\right)$$

I used Maple to try and see if this expression simplifies, but it does not seem to. Numerically, plugging in the above values does yield $\angle UFO = 75.000000°$.

Answer 4

This is a solution, though not a solution in the spirit intended.

I haven't figured out how to do this problem with synthetic geometry, but I know the answer is $75^{\circ}$. I did it with analytic geometry, assuming O is the point $(0,0)$ and E is the point $(1,0)$. I wrote this little python script to perform the calculations:

from  math import *
a = tan(80pi/180)    # ON: y = ax
b = tan(60pi/180)    # OF: y = bx
c = tan(145pi/180)   # EU: y = c(x-1)

d = tan(140pi/180)   # EN: y = d(x-1)
x1 = c/(c-a)          # U(x1,y1) is intersection of ON and EU
y1 = ax1

x2 = d/(d-b)          # F(x2,y2) is intersection of OF and EN
y2 = bx2
print('U:',x1,y1)
print('F:',x2,y2)
#OF = (x2,y2)             # vectors
#FU = (x2-x1,y2-y1)
dot = x2(x2-x1)+y2(y2-y1)     #dot product
of = sqrt(x22+y22)          # lengths
fu = sqrt((x1-x2)2+(y1-y2)2)
theta = acos(dot/(offu))180/pi  # angle between OF and FU

print('theta:', theta)

and it produced the output

    U: 0.10989699564506068 0.623256833432439
    F: 0.3263518223330698 0.5652579374235681
    theta: 75.00000000000004

EDIT

• The script has been edited to correct the mistake pointed out in the comments. It would be interesting to know if the answer is exactly $75^{\circ}$ or just $75^{\circ}$ to a high degree of precision.

• Now that I've read Rahul's comment on adventitious triangles, I'd bet it's exactly $75^{\circ}.$ A worked-out solution to a similar problem is given here but I haven't gone through it yet.

• I've found a bunch of references for this topic. I have not done more than glance at them.
  
  
  The Mathematical Gazette Vol. 62 No. 421 (Oct. 1978) has two articles on the subject: "Last words on adventitious angles," by D. A. Quadling (editor) and "Adventitious quadrangles, a geometrical approach," by J.F. Rigby. (Both papers can be accessed in JSTOR.)
  
  The first paper seems to deal only with the case of adventitious isosceles triangles, which was the first problem considered historically.
  
  The second paper extends the discussion to general triangles. Note that in the OP's problem, we really don't need the point N. It is there only so we may deduce $\angle UEF = 5^{\circ}$. If this is given, we can dispense with N, and deal with the quadrangle UFEO. This is the problem Rigby considers. This paper is a summary of a longer paper, "Multiple intersections of diagonals of regular polygons, and related topics," also by Rigby, in Geometriae Dedicata June 1980, Volume 9, Issue 2, pp 207–238. This does not seem to be available online.
  
  Apparently, Rigby sought elementary geometry proofs for all the adventitious quadrangle problems, but was unable to dispose of some cases. This paper claims to close the gap, but just looking at the diagrams makes my head hurt.
  
  Kevin Brown gives a trigonometric/algebraic approach in his Math Pages. Although the solutions won't be as elegant as the geometrical ones, they look more interesting to my taste. For example, they result in curious identities like $$ \tan(10^{\circ})= \tan(20^{\circ})\tan(30^{\circ})\tan(40^{\circ}) $$

Answer 5

None of the other answers is purely synthetic. Let me post one.

First of all, we easily calculate $\angle FEU = 5^\circ$.

Let $P$ be a point on $EU$ such that $PE=PF$. Then $\angle PFE = \angle FEP = 5^\circ$ and so $\angle FPU = \angle PFE + \angle FEP = 10^\circ$.

Let $Q$ be a point of $PU$ such that $PQ=QF$. Then $\angle QFP = \angle FPQ = 10^\circ$ so $\angle FQU = \angle QFP + \angle FPQ = 20^\circ$.

Build an equilateral triangle $PQR$. Also, let the circle centered at $P$ with radius $PE=PF$ intersect $OE$ at $S$ (so in particular $PS=PF$). Note that $$\angle RPS = \angle FPS - \angle FPQ - \angle QPR = 2\angle FES - 10^\circ - 60^\circ = 2\cdot 40^\circ - 70^\circ = 10^\circ = \angle FPQ.$$ This along with $PQ=PR$ and $PF=PS$ shows that triangles $FPQ$, $SPR$ are congruent. This shows that $RS=FQ$.

Now we can prove that $\angle FQR = 140^\circ = \angle QRS$. Perhaps the fastest way is to note that $F, P, R$ lie on a circle with center $Q$ so $\angle FQR = 2\angle FPR = 2 \cdot (\angle FPQ + \angle QPR) = 140^\circ$. Similarly, $\angle QRS = 140^\circ$. So $\angle SQR = 90^\circ - \frac 12\angle QRS = 20^\circ$ hence $\angle FQS = \angle FQR - \angle SQR = 140^\circ - 20^\circ = 120^\circ$. We prove similarly that $\angle FRS = 120^\circ$. Hence $FQRS$ is inscribed in a circle, marked on the picture in red. (It is in fact an isosceles trapezoid but we don't need that.)

Also, $\angle SOF + \angle FQS = 60^\circ + 120^\circ = 180^\circ$, so $OFQS$ is cyclic. Hence $O$ also lies on the red circle.

Since $\angle FOU = 20^\circ = \angle FQU$, it follows that $OUFQ$ is cyclic. This means that $U$ also lies on the red circle.

Phew! Now we can easily calculate $\angle UFO$. Note that $\angle QUF = \angle QRF = 20^\circ$ and $\angle OUE = 180^\circ - \angle EOU - \angle UEO = 180^\circ - 80^\circ - 35^\circ = 65^\circ$. Hence $$\angle UFO = 180^\circ - \angle FOU - \angle OUF = 180^\circ - 20^\circ - (65^\circ + 20^\circ) = 75^\circ.$$

Answer 6

UFO Problem Solved

Given
$∠ONE=60°, ∠NOF=20°,∠FOE=60° \;\&\; ∠UEO=35°$

• From $∆NOE\\$
  $∠NOE + ∠OEN + ∠ENO = 180°\\ (20° + 60°) + (35° + ∠UEF) + 60° = 180°\\ ∠UEF = 5\\$
  So, $\boxed{∠OEN = 40°}\qquad{(1)}\\$

NOW

    ON/Sin(∠OEN) = EN/Sin(∠NOE) = OE/Sin(∠ONE)
ON/Sin(40) = EN/Sin(∠80) = OE/Sin(60) 

ON = (OE*Sin(40))/Sin(60)             &                EN = (OE*Sin(80))/Sin(60) 

ON = 0.742227*OE                                   ----(2a)
 &          
EN = 1.137158*OE                                   ----(2b)

From ∆NOF

    ∠ONF + ∠NFO + ∠FON = 180°
60° + ∠NFO + 20°  = 180°

∠NFO =100°

Using proverty if triangle

    ON/Sin(∠NFO) = NF/Sin(∠NOF) = OF/Sin(∠ONF)
(0.742227*OE )/Sin(100) = NF/Sin(20) = OF/Sin(60)                 Using (2a)

NF = (0.742227*OE*Sin(20) )/Sin(100)  

NF=0.257772*OE                                                ---------------(3)

From ∆NUE

    ∠NUE + ∠UEN + ∠ENU = 180°
∠NUE + 5° + 60°  = 180°

∠NFO =115°

Using property of triangle

    UN/Sin(∠UEN) =EN/Sin(∠NUE) =UE/Sin(∠UNE)
(UN )/Sin(5) =(1.137158*OE)/Sin(115) =UE/Sin(60)                   Using (2)

UN=(1.137158*OE*Sin(5))/Sin(115)   

UN=0.109355*OE                               ---------(4)

From ∆NUF

    ∠UNF = 60°=  ∠ONE (Given)
∠UNF + ∠NUF + ∠UFN = 180°

60° +∠NUF + ∠UFN = 180°

∠NUF + ∠UFN =120°

∠NUF = 120° - ∠UFN                    ---------------------(5)

UN = 0.109355*OE                                           Using (4)
NF = 0.257772*OE                                           Using (3)

Using Property of Triangle

    UN/Sin(∠UFN) = NF/Sin(∠NUF) = UF/Sin(∠UNF)
(0.109355*OE)/Sin(∠UFN) = (0.257772*OE)/Sin(120°-∠UFN) = UF/Sin(60) 

Sin(120°-∠UFN)/Sin(∠UFN) =(0.257772*OE)/(0.109355*OE) 

Sin(A-B)=Sin(A)*Cos(B)-Sin(B)*Cos(A)

    (Sin(120)*Cos(∠UFN)-Sin(∠UFN)*Cos(120))/Sin(∠UFN) =2.357203
(0.866025*Cos(∠UFN)-Sin(∠UFN)*(-0.5))/Sin(∠UFN) =2.357203

(0.866025*Cos(∠UFN))/Sin(∠UFN) +0.5=2.357203

0.866025/Tan(∠UFN) =1.857203

0.866025/1.857203=Tan(∠UFN)

0.466306=Tan(∠UFN)

∠UFN=〖Tan〗^(-1)(0.466306)

∠UFN=25° =                               -----------------(6)

From ∆NOF

    ∠ONF + ∠NFO + ∠FON = 180°
60° + ∠NFO + 20°  = 180°

∠NFO =100°

∠UFN + ∠UFO =100°

25°+ ∠UFO =100°                                      Using (6)

∠UFO =75°

Answer 7

UFO problem solved with the help of given condition`