10

Each prime number greater than $9$, written in base $10$, ends with one of the four digits $1,3,7,9$. Therefore, each ten can be classified according to which of these four digits, summed to the ten, yields to a prime number.

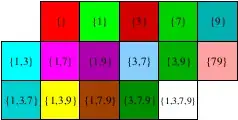
For example, for the first ten we have $1 \rightarrow \{1,3,7,9\}$. In fact, $10+1$, $10+3$, $10+7$ and $10+9$ are all primes. Conversely, for the twentieth ten the association reads $20 \rightarrow \{\}$, since there are no primes between $200$ and $209$.

It is easy to see that each ten is associated to one (and only one) group of symbols, chosen among the following $16$ distinct alternatives: $\{\}$, $\{1\}$, $\{3\}$, $\{7\}$, $\{9\}$, $\{1,3\}$, $\{1,7\}$, $\{1,9\}$, $\{3,7\}$, $\{3,9\}$, $\{7,9\}$, $\{1,3,7\}$, $\{1,3,9\}$, $\{1,7,9\}$, $\{3,7,9\}$, $\{1,3,7,9\}$.

For the sake of simplicity, we can identify each of these $16$ distinct groups of symbols with a single symbol, or with a single color, as illustrated below:

enter image description here

Each of these colors represents how many prime numbers there are in one ten (and which ones). In practice, we have just split the complexity of primes into tens and colors.

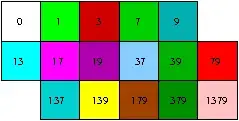
This allows us to rearrange the colors within the Pascal's triangle, by means of the associated ten, obtaining the following scheme (the numbers in the squares represent the tens):

enter image description here

The complexity of the primes sequence has been now split into rows, diagonals and colors.

An advantage of such representation is that it mixes groups of primes related to far tens, allowing maybe to identify patterns and/or to dig out connections among already known integer sequences. The clear disadvantage is that the patterns on this triangle depend on which base we use.

I partially introduced this representation of prime numbers here, but I am not sure whether these further developments overlap with some very well known technique (e.g. Sieve of Eratosthenes?).

In conclusion, just not to re-invent the wheel, my question is:

Do you know if such representation has been already devised? In that case, could you please give me some reference?

Sorry for naivety and incorrectness, and thank you very much for your suggestions and comments!

NOTE: The conjecture contained in the following EDIT is FALSE, and there is a mistake in the code! Please, if you have a good software to produce the picture, please tell me! Thanks! (Thanks also to Paul!)

EDIT: To reply to some comments, and adopting this somehow enhanced color code,

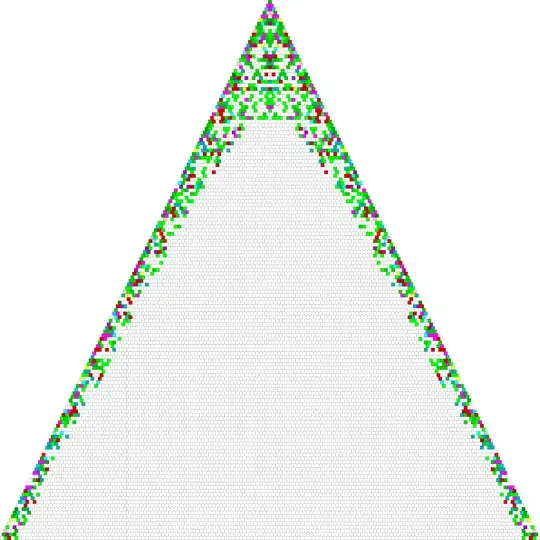
enter image description here

I produced the following plot (omitting the first ten)

enter image description here

I hope that there is not some mistake in my code! However,

It is conjectural that, for very big numbers, there cannot be colored squares other than on the outer edge of the triangle,

which means that, beyond a certain integer $N$, the primes will all fall in tens (powers of ten) that can be written in the form $t=\binom{n}{k}$, where $k$ is $2,3,4$ maximum. This may lead to interesting consequences, considering that this property should not change much according to the base, and primes are infinite.

As mentioned in the NOTE, this picture is actually incorrect. It should look like this:

enter image description here

Still working on it!

  • 1
    The most interesting thing is, it looks symmetric! – tarit goswami Aug 27 '18 at 12:58
  • 1
    @taritgoswami Well, this is a property of Pascal's triangle. –  Aug 27 '18 at 13:00
  • I though you have classified numbers and colored same type of numbers with single color. I mean the colors are symmetrically appeared in the triangle. – tarit goswami Aug 27 '18 at 13:15
  • It is very unlikely that any visual pattern emerging by the prime numbers holds until very large primes. For the first primes, even for some hundred or some thousand primes, easy patterns (or configurations that are at least similar to some easy pattern) can well be possible, but the behaviour of the primes is so complex that the pattern almost surely will eventually vanish when the primes became bigger. Additionally, many easy seeming question about prime numbers are still open, for example, are there infinite many primes of the form $n^2+1$ ? – Peter Aug 27 '18 at 17:17
  • 1
    When there are no primes in a block of $10$, like between $200$ and $209$, you should denote this $20 \to {}$, not $20 \to {0}$. The notation you use suggests that $200$ is prime. The former notation, $20 \to {}$ correctly suggests that the set of primes is the empty set, i.e., there are no primes. – Caleb Stanford Aug 27 '18 at 19:52
  • @6005 True, thanks for your observation. However, since later I use a color (or whatever other symbol) to denote the group, this imprecision is not too severe. Thanks again, now I edit! –  Aug 27 '18 at 19:54
  • I'm not entirely sure I get the need for Pascal's triangle here. I get that you want some structure to compare "far away" tens, but otherwise it just feels unnecessary. You could just as well make an analogue of the prime spiral: http://mathworld.wolfram.com/PrimeSpiral.html

    Unfortunately, your colors will become mostly red after a while, given that primes become exceedingly sparse.

     – Alex R. Aug 28 '18 at 10:53
  • @AlexR. Thanks for your comment. Sure, I agree with the sparseness argument. The Pascal triangle comes because the tens, in this context (i.e. once removed the digits that cause the ten to be prime), they behave like integers, and the first thing I thought was to organize them as the integers in the Pascal triangle. But sure I have to think more about it. My concern was mainly if someone has already done this, and/or if it is analogous to some other method/tool to study the primes. Thanks again! –  Aug 28 '18 at 12:05
  • @AndreaPrunotto: I would strongly recommend trying a spiral, as it grows like $n^2$ with respect to it's width $n$. – Alex R. Aug 28 '18 at 16:57
  • I would look at this in duodecimal and hexadecimal. Very interesting regardless. – Robert Soupe Aug 28 '18 at 17:16
  • @AlexR. Sure, any suggestion how to implement/code it? PS. I added a bigger plot with some observations. Thanks again. –  Aug 28 '18 at 18:07
  • @RobertSoupe Yes! I will work on it! Thanks! –  Aug 28 '18 at 18:08
  • 1
    @AndreaPrunotto: This is uncannily complete in many languages: https://rosettacode.org/wiki/Ulam_spiral_(for_primes)

    So instead of highlighting primes, highlight the ten's with your gradations.

     – Alex R. Aug 28 '18 at 18:30
  • 2
    @AndreaPrunotto I tried to reproduce the image and I don't have the big white area. I think your code doesn't handle big numbers (numbers above $2^{31}-1$, the maximum value of a signed 32-bit integer) well. Which programming language are you using? You must use some big number library, which may be already available in the language you're using, or otherwise you can probably find it online somewhere. – Paul Aug 28 '18 at 21:19
  • @Paul True, I have just realized it. I used R, but I am not a dragon in coding. Can you show me how it appears, or the code? Which language do you use? Thanks for your comment! –  Aug 28 '18 at 21:30
  • @AlexR. Sure I will do it! Thanks again!!! –  Aug 28 '18 at 21:33
  • 1
    @AndreaPrunotto I have no knowledge of R, but I'm using Mathematica. My code is colors = Prepend[ColorData["DarkBands"] /@ (Range[0, 14]/14), White]; group[k_] := FromDigits[Boole[PrimeQ[10 k + {1, 3, 7, 9}]], 2] + 1; Table[colors[[group[Binomial[n, k]]]], {n, 1, 40}, {k, 1, n - 1}] // Grid – Paul Aug 28 '18 at 21:45
  • @Paul Thanks for sharing, Paul! –  Aug 28 '18 at 22:01
  • 1
    @AndreaPrunotto Maybe an idea to update your question so other people don't waste their time on the conjecture if they don't read the comments. – Paul Aug 29 '18 at 14:35
  • @Paul Yes. I am producing finally a correct plot and I will edit. Good idea, thanks! Done –  Aug 29 '18 at 14:46
  • @AlexR. I've followed your suggestion about the spiral. Please, have a look here https://math.stackexchange.com/q/2903194/559615, you might be interested to see the (hypnotic) images I obtained! Also, if you have any idea how to analyze them let me know. Thanks! –  Sep 03 '18 at 19:07

0 Answers0