The first part of the proof describes construction of a bowl type shape comprising a base pentagon $A$ and five adjacent pentagons $B, C, D, E, F$, which form a 'side wall' - a rigorous argument could be made for this using 'trihedral angles', or by considering intersections of cones.
However the subsequent part of the proof where an upper 'side wall' is constructed is problematic and cannot be 'fixed'. The proof only makes use of the bilateral symmetry which arises when two pentagons are joined along a common edge - however it doesn't make use of the much stronger symmetry where three pentagons are joined at a common vertex. It considers the planar angles inside the pentagons but it does not consider the dihedral angles between the pentagon planes.
To see the problem consider Fig 1 below which shows a 'schematic' diagram (not geometrically accurate) indicating the relative positions of the various pentagons and edges. Assume we have already constructed a lower bowl (pentagons $A, B, C, D, E, F$) and established its $72^\circ$ rotational symmetry and its bilateral symmetry through any vertical plane passing through its center and an edge between two pentagons in its side wall. Our objective is to build an upper side wall by adding the five pentagons $G, H, I, J, K$ into the planes of the lower corners of the zigzag of the bowl. The bilateral symmetry of adjacent pentagons $B$ and $C$ in the bisector plane $P$ of $e_6$ assures that pentagon $G$ can successfully be inserted in the lower corner at $W$ since it implies the angle in the lower corner at $W$ is $\theta = 108^\circ$. Likewise $H, I, J, K$ can be inserted into the other four lower corners.
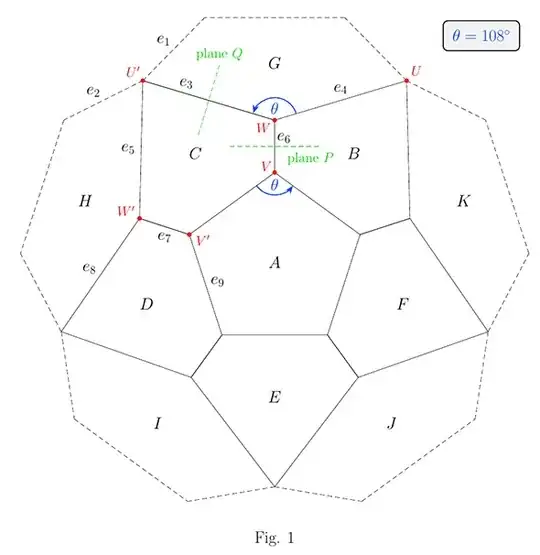
As Gowers says we now need to show that each of $G, H, I, J, K$ shares common edges with the ones before and after it in this list (cyclically), so that they form a ring. By symmetry it suffices to consider $G$ and $H$. Thus we require to show that edges $e_1$ and $e_2$ in Fig 1 are coincident.
The only information we have on $G$ is that its edge $e_3$ is common to $C$, and its edge $e_4$ is common to $B$. The only information we have on $H$ is that its edge $e_5$ is common to $C$, and its edge $e_8$ is common to $D$.
The proof now claims that under reflection in plane $P$ :
"$H$ maps to a pentagon that shares an edge with $A$ and $C$"
However although we can deduce the image $H'$ of $H$ shares edge $e_7$ with $C$, since edge $e_5$ of $C$ maps onto edge $e_7$ of $C$, we cannot deduce $H'$ shares an edge with $A$ since the only information from which that could follow would be that $H$ shares edge $e_1$ with $G$ (ie. that $e_1 = e_2$) and then apply $G' = A$ to deduce $H'$ shares edge $e_9 = e_1'$ with $A$. There are no other avenues that lead to $H'$ sharing an edge with $A$. However this antecedent, ie. $H$ sharing edge $e_1$ with $G$, is what we are trying to prove - it is thus a circular argument. Based on the information we have, we cannot assume that $H$ shares any edges with $G$.
We could attempt a variation - again observing $H'$ must contain $e_7$ as an edge, as $e_7$ is the image of $e_5$. This would tell us $H'$ is some pentagon which has $e_7$ as an edge, from which we might be tempted to conclude $H'$ is either $C$ or $D$, and hence that it must be $D$ as certainly $H' \neq C$ (for $H' = C$ would imply $H = C' = C$ which is clearly false). However we have not shown $H'$ is a pentagon within the figure, we just know it is a pentagon somewhere in space - to locate it within the figure we would require it to contain two adjacent edges within the figure.
Another variation we could try is when inserting $H$, instead of aligning it to edges $e_5$ and $e_8$ in lower corner $W'$, instead align it with $e_1$ and $e_5$. This is possible since we have already inserted $G$ and the mirror image symmetry in plane $Q$ bisecting $e_3$ implies the angle between $e_1$ and $e_5$ is the mirror image of the pentagonal angle $\theta$ in $B$ at $W$. We would then require to show an $H$ positioned in this way meets $D$ along edge $e_8$ (so in Fig 1, $H$ is now potentially broken away from $e_8$ but it is joined to $e_1$ along $e_2$). If we can show this then $H$ would both fit into the zigzag and share its right edge with the left edge of $G$, as required. This new positioning of $H$ is the mirror image in plane $P$ of $D$, since $H$ is situated in a corner formed by $G$ and $C$ whilst $D$ is situated in the mirror image of this corner at $A$ and $C$. Label the edge of $H$ that is potentially broken away from $e_8$ as $e_{10}$. Then $e_{10}' = e_8$, since these are mirror images (or as this is getting slightly tricky to visualize : $e_{10}$ is the next edge in $H$ after $e_1$ and $e_5$, and then apply the map to this statement to arrive at $e_{10}'$ is therefore the next edge in $D = H'$ after $e_1' = e_9$ and $e_5' = e_7$ and then observe that the latter statement implies $e_8$). If we use $H$ having edges $e_1$ and $e_5$ to conclude $H'$ has edges $e_1' = e_9$ and $e_5' = e_7$ and hence that $H' = D$ and $H = D'$ we only get back to information we already know, and we are again going around in a circle, never arriving at the desired conclusion, which is $e_{10} = e_8$.
Another way to look at the problem is to consider that with the angle between edges $e_1$ and $e_5$ being $\theta$, and with the lower corner angle at $W'$ also being $\theta$ then if the three edges $e_1$, $e_5$, $e_8$ were coplanar they would form three consecutive sides of a pentagon, which could then be completed with a further two sides to form the required $H$. However we are not able to prove this coplanarity with this proof approach.
One way to obtain a formal proof is using 'trihedral angles'. For the present purpose define a 'trihedral angle' (TA) as the compound of three planar angles and three dihedral angles formed by three planes whose intersection is a single point. Assume the angles are all in the range $(0, 180)$, so that the figure formed by the TA as we view it is convex. Define an 'equilateral trihedral angle' (ETA) as one with three equal planar angles $\theta$. Then the following results hold :
(a) if we have 3 planes $\Gamma_1, \Gamma_2, \Gamma_3$ as in Fig 2 (i) with $\theta \in (0, 180)$ and $\Gamma_2$ and $\Gamma_3$ both making dihedral angle $\delta \in (0, 180)$ with $\Gamma_1$, then if $\epsilon$ is the dihedral angle between $\Gamma_2$ and $\Gamma_3$ then $\epsilon = \delta$ iff :
\begin{equation}
\cos \delta = \frac{\cos \theta}{1 + \cos \theta} \label{eq:delta} \tag{1}
\end{equation}
or equivalently
\begin{equation}
\cos \theta = \frac{\cos \delta}{1 - \cos \delta} \label{eq:theta} \tag{2}
\end{equation}
For a given $\theta \in (0, 180)$, a solution $\delta \in (0, 180)$ to (\ref{eq:delta}) exists iff $\theta < 120$, and is unique and in the range $(60, 180)$.
(b) A TA is equilateral iff its 3 dihedral angles are equal.
(c) if we have a planar angle $\theta \in (0, 180)$ with two dihedral angles $\delta \in (0, 180)$ to either side as in Fig 2 (ii), and if (\ref{eq:delta}) holds, then all three planar angles equal $\theta$ and all three dihedral angles equal $\delta$, so that the TA is an ETA.
(d) if we have a dihedral angle $\delta \in (0, 180)$ with two planar angles $\theta \in (0, 180)$ to either side as in Fig 2 (iii), and if (\ref{eq:delta}) holds, then all three planar angles equal $\theta$ and all three dihedral angles equal $\delta$, so that the TA is an ETA.
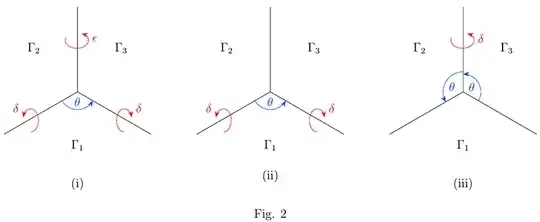
To prove (a) we can set up a coordinate system with $\Gamma_1$ in the $xy$-plane, and use the Rodrigues Rotation Formula (or equivalent 2D transform) to rotate a unit normal $\underline{\mathbf{u}}$ to $\Gamma_3$ by $(180 - \theta)^\circ$ about the $z$-axis to obtain a unit normal $\underline{\mathbf{v}}$ to $\Gamma_2$, and then solve $\cos \delta = -\underline{\mathbf{u}} \cdot \underline{\mathbf{v}}$ for $\cos \delta$. Similarly '$\Rightarrow$' of (b) can be proved using vector rotation.
An ETA with $\theta = 60^\circ$ and $\delta = \arccos (1/3)$ is formed at the apex of a tetrahedron, and if we move the apex up and down to varying altitudes $h$ then $\theta$ varies from $120^\circ$ to $0^\circ$ and $\delta$ from $180^\circ$ to $60^\circ$ as $h$ increases, and this generates all possible ETA's. With $\theta = 90^\circ$ we get a cubic ETA with $\delta = 90^\circ$, and with $\theta = 108^\circ$ we get a pentagonal ETA with $\delta = \arccos (-1/\sqrt{5})$, but we can have intermediate ETA's for which there is no corresponding regular polygon. At a hexagon ($\theta = 120^\circ, \delta = 180^\circ$) we reach the limit and the ETA becomes flat.
To construct the side wall pentagons of the bowl we start with only the base pentagon $A$, and at vertex $V$ add two planes $B$ and $C$ aligned on the edges of $A$ to the right and left of $V$ (as in Fig 1 above), and then raise both $B$ and $C$ up to make dihedral angle $\delta = \arccos (-1/\sqrt{5})$ with $A$. Then by (\ref{eq:delta}) above the dihedral angles between those two planes is $\delta = \arccos (-1/\sqrt{5})$, and (c) applies, so that the TA formed by the three planes at $V$ is an ETA with all three planar angles $\theta$ and all three dihedral angles $\delta$.
Due to the planar angles $\theta$ in planes $B$ and $C$ at $V$ we can cut these planes to pentagons identical to $A$, producing a 3-way symmetric figure of three pentagons joined at a common vertex, with all three dihedral angles $\delta$ and all fifteen planar angles $\theta$. By symmetry the line of intersection of $B$ and $C$ lies in the central vertical plane through the center of $A$.
We can now apply a similar construction at the next vertex $V'$ of $A$, and the right hand pentagon created will coincide with $C$ since it makes dihedral angle $\delta$ with $A$. Repeating this for the remaining three vertices of $A$ we complete a lower bowl. We could have proceeded CW instead of ACW and figure created would be the same. The figure has $72^\circ$ rotational symmetry and it has bilateral symmetry through any vertical plane passing through the center of $A$ and an edge between two pentagons in the side wall.
To construct the upper side wall consider the five planes formed by edge pairs such as $e_3$ and $e_4$ that meet in the lower corners of the zigzag. (d) applies at $W$, so dihedral angles at $e_3$ and $e_4$ are $\delta$ and angle between $e_3$ and $e_4$ is $\theta$, and the trihedral angle at $W$ is convex, viewing from the inside of the lower bowl. This applies at all the five lower corners. Now consider how two adjacent of these five planes meet, for example at $U'$. At $U'$ (c) applies, so we have an ETA($\delta$, $\theta$) formed by planes $C$, $G$, $H$, and this again is convex. We can cut the line $G \cap H$ above $U'$ to have length $l$, the common pentagon side length, and do likewise for the other four intersections, so that each plane $G, H, I, J, K$ now forms an upturned pentagon with four lower side lengths $l$, and three lower angles $\theta$ between them, which means it must be a regular pentagon of side $l$. This completes a ring of pentagons forming an upper side wall to give an eleven sided figure with all dihedral angles $\delta$.
An alternative way to create the upper side wall is to use 'partial bowls'. For example $B$ forms the base of a partial bowl with three contiguous side wall pentagons $C, A, F$ since the dihedral angles are all $\delta$ - hence it can be completed to a full bowl. This adds pentagons in the upper side wall at positions $G$ and $K$. Now $C$ forms the base of a partial bowl with four contiguous side wall pentagons $D, A, B, G$ , again since the dihedral angles are all $\delta$, and hence it can be completed to a full bowl, which adds a pentagon into the upper side wall at position $H$. Completing partial bowls at $D$ and $E$ adds a further two pentagons $I$ and $J$, and when we come to $F$ a full bowl has already been formed with $E, A, B, K, J$.
The ring of five pentagons in the upper side wall is a partial bowl and thus can be completed to a full bowl by addition of a base pentagon, a 'cap', thus creating a closed figure comprising twelve pentagon faces, divided into identical upper and lower bowls which join along the zigzag. Every dihedral angle is $\delta$ and by the construction every face has five neighbours with which it forms a bowl. For example in the upper side wall a pentagon forms a bowl with the two pentagons below it, the two pentagons to either side of it, and the pentagon cap. The interior of the figure contains 20 identical ETA($\delta$, $\theta$)'s, one at each vertex.
By the symmetry of the lower bowl the base pentagon of the lower bowl is parallel to, and (in the plan view) concentric with and aligned to the pentagon formed by the lower zigzag corners at points such as $W$. It is also parallel to, and (in the plan view) concentric with and rotated $36^\circ$ from (equivalently inverted from) the pentagon formed by the upper zigzag corners at points such as $U$. Since the upper and lower bowls share the same zigzag, similar statements can be made for the base of the upper bowl, so that the upper and lower bowl bases are parallel, and (in the plan view) concentric with and inverted from one another. From the symmetry properties of the two bowls the entire figure has $72^\circ$ rotational symmetry about the central vertical axis and it has bilateral symmetry about any vertical plane through its center which contains the boundary edge between two adjacent side wall pentagons.
We can now re-orient the figure to place an arbitrary face $F$ in the position of $A$ in Fig 1. Then on retracing the figure from the base $F$ we must reconstruct a figure congruent to the original Fig 1, since at every stage the same dihedral angles $\delta$ are present throughout, completely determining the positions of all the pentagons. For example when we retrace the lower bowl around $F$ we reconstruct the original lower bowl. When we build the upper side wall on top of that we reconstruct the original side wall. Thus we have a 12-fold symmetry of the figure wrt its 12 pentagonal faces.
We could now define the opposite $\overline{F}$ of a face $F$ as the unique face parallel to it, and the opposite $\overline{E}$ of an edge $E$ as the unique edge parallel to it. The opposite $\overline{V}$ of vertex $V$ could be defined as the opposite vertex of $V$ in the decagon formed by $F$ and $\overline{F}$ in the plan view, where $F$ is any face containing $V$ (this would be consistent for all three possible choices of $F$).
Another situation where using the full symmetry available is helpful is when proving the dodecahedron contains a compound of five cubes, whose edges are the 60 face diagonals. Here we find that for any face diagonal there are exactly three other face diagonals parallel to it, and these define an equilateral rhombic cylinder (ERC) of side length $\Phi l$. To prove it is a cube we could try and prove adjacent sides of the rhombus are perpendicular - but a much easier method is to use the 12-fold symmetry of the dodecahedron to deduce $V\overline{V}$ is of equal length for all vertices V and hence that the four interior diagonals of the ERC are equal, and thus the diagonals of the rhombus are equal and hence the rhombus is square, and the ERC a cube.
A similar process of completing a partial base figure can be used in constructing the icosahedron, where the base figure is a pentagonal pyramid with equilateral triangle slopes - any pair of equilateral triangles with the right dihedral angle can be completed to such a pyramid on either side.

