Why does the Eigen decomposition of the covariance matrix of a point cloud give its orientation?

Question

I am working with point clouds and one of the problems I had to face was to find the orientation of a given cluster. Most algorithms I have found suggest that one must first calculate the centroid of the cloud and, using that, to compute the covariance matrix. Performing the Eigen decomposition on the co-variance matrix gives us three vectors that correspond to each of the three axis that give the orientation of the object. I have successfully implemented the algorithm, but I wish to know how and why this works specifically.

Answer 1

Let's say you have a (centered) point cloude $p_i,i=1,...,n$ and you want to know the orientation of the cloud. How can we formalize this question? E.g. we could ask "in what direction the point cloud is spread out the most?". This means, which unit vector $v\in\Bbb R^n$ gives the sequence

$$x_i := v^\top p_i,\quad i=1,...,n,$$

with the largest variance. Here, $v$ is the direction in which we want to check "how spread out" the cloud is, and $v^\top p_i$ is the projection of the point onto this direction. The variance of the sequence is computed via

\begin{align} \frac 1{n-1} \sum_{i=1}^n x_i^2 &= \frac1{n-1} \sum_{i=1}^n(v^\top p_i)^2 \\ &= \frac1{n-1} \sum_{i=1}^n(v^\top p_i)(p_i^\top v) \\ &= \frac1{n-1} \sum_{i=1}^n v^\top(p_i p_i^\top) v \\ &= v^\top\underbrace{\left(\frac1{n-1} \sum_{i=1}^n p_i p_i^\top\right)}_{=:\,P} v = v^\top P v. \end{align}

So you try to find the unit vector $v$ which maximizes $v^\top P v$, where $P$ turns out to be the covariance matrix of your point cloud. If you are familiar with Rayleigh quotients, then it should be clear to you that this is exactly the case when $v$ is the eigenvector to the largest eigenvalue of $P$. You then have

$$v^\top P v = v^\top \lambda_\max v = \lambda_\max \cdot \underbrace{v^\top v}_1 = \lambda_\max.$$

So, on top of that, the corresponding eigenvalue gives you the variance along the direction $v$.

The argumentation works the same for the "least spread out" direction, and one can argue that the other eigenvectors belong to some intermediate axes.

Answer 2

A covariance matrix $\Sigma$ is symmetric, so there’s a corresponding quadric hypersurface given by the implicit equation $\mathbf x^T\Sigma\mathbf x=1$. Every real symmetric matrix is orthogonally diagonalizable and, moreover, that basis gives the principal axes of the quadric. So, the eigendecomposition of $\Sigma$ tells you how this quadric is oriented, among other things.

The covariance matrix of a point cloud captures how the “spread” of random variables that make up the vector interact pairwise. The eigendecomposition in a sense finds an orthogonal transformation of the coordinate system—an orientation for it—that completely decorrelates the data.

Answer 3

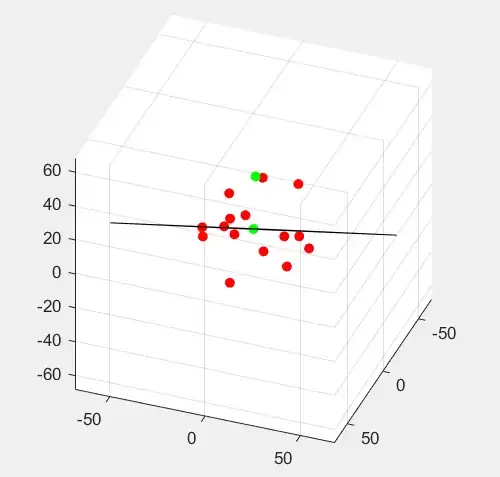
function [vnorm, Ds] = fitNormVector(pts)
    %fitNormVector 输入为 n by m 代表Rn空间中的m个点的坐标
    %   用svd分解covariance得到的最小的eigvalue的eigvector 为 n维的normal
    mtd = pts - mean(pts,2);
    [v,d]=eig(mtd*mtd');
    [~,ind] = sort(diag(d));  % 按小到大给diag排序
    Ds = d(ind,ind); % 排序后的diag矩阵
    vnorm = v(:,ind(1))*max(abs(mtd(:)));

    w = null(vnorm');  % 求垂直于normal的核空间的向量轴
    scatter3(mtd(1,:),mtd(2,:),mtd(3,:),'filled','r')
    pbaspect([1 1 1]); daspect([1 1 1]); % 保持绘图比例
    hold on
    scatter3(vnorm(1),vnorm(2),vnorm(3),'filled','g'); % 画法向量
    scatter3(0,0,0,'filled','g'); % 画原点(已经平移到中心)
    [P,Q] = meshgrid(-50:10:50); % Provide a gridwork (you choose the size)
    X = w(1,1)*P+w(1,2)*Q; % Compute the corresponding cartesian coordinates
    Y = w(2,1)*P+w(2,2)*Q; %   using the two vectors in w
    Z = w(3,1)*P+w(3,2)*Q;
    surf(X,Y,Z,'FaceColor','none')
end

The Matlab code example above will plot the following figure once called by

[v,d]=fitNormVector(rand(3,15)*50)

This plane is the best fitting plane close to all points.

This is the widest spreaded view of points.