18

What algorithms exist to draw planar graphs without edge crossings in a way that they are easy to interpret by humans?

There are multiple algorithms that can handle any planar graph, such as Schnyder's algorithm or Chrobak-Payne. These typically produce a result that is not very useful.

Here's an example.

The graph corresponding to this polyhedron,

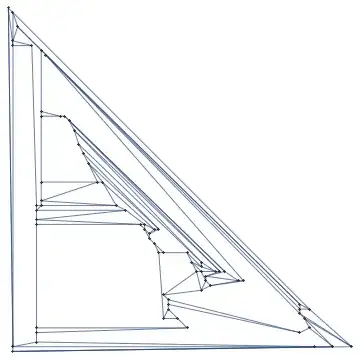
enter image description here

looks like this with Schnyder's algorithm:

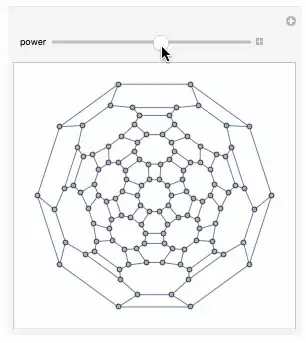
enter image description here

It looks like this with whatever Mathematica has built in:

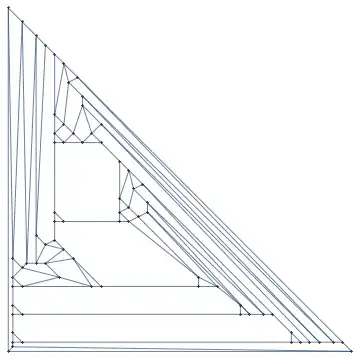
enter image description here

What seems to work better in practice is using the Tutte embedding. For this graph it gives:

enter image description here

I chose this graph specifically because it demonstrates in what way the Tutte layout is often not very good: the points in the middle are squeezed together.

Another problem is that it only works for 3-vertex-connected graphs. It may be possible to work around this sometimes, e.g. the Maple help says that Maple will try to construct a similar but 3-connected graph to use for computing the layout. It does not detail the procedure though.

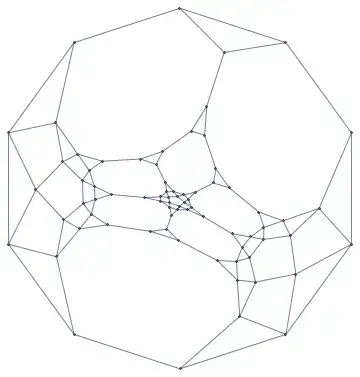
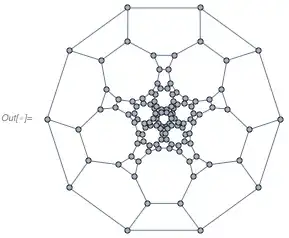
Note that this graph clearly has a nice drawing, e.g.

enter image description here

One could do even better by manual rearrangement. (This drawing is obtained by manual adjustment of a layout from Mathematica's GraphData database.)

Questions:

My goal is to plot planar graphs in a "visually pleasing" way, i.e. in a way that humans can interpret them easily.

  • What algorithms are there that are useful for this?

  • The Tutte layout often works well. How can one make it useful for non-3-connected graphs? (References would be nice.)

  • Are there algorithms that lay out the graph in 3D, on the surface of a sphere? I am hoping to solve the problem of Tutte squeezing the middle points together.

  • Are there any algorithms that use curved edges to make the visualization clearer? The problem with straight line drawings is that edges sometimes make a very small angle. It may be that there is no way around this, but to use curved edges.

Notes:

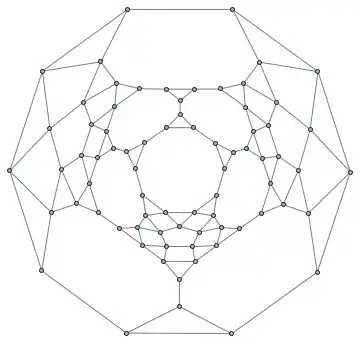
I am aware that a simple force-directed layout algorithm often produces good results in 3D. E.g. for the above polyhedral graph we get:

enter image description here

For others, it doesn't work well at all. Here's the edge list of a difficult instance:

{{1, 2}, {1, 6}, {1, 7}, {2, 3}, {2, 6}, {2, 7}, {2, 8}, {3, 4}, 
 {3, 7}, {3, 8}, {3, 9}, {4, 5}, {4, 8}, {4, 9}, {4, 10}, {5, 9}, 
 {5, 10}, {6, 7}, {7, 8}, {8, 9}, {9, 10}, {3, 5}, {4, 2}, {6, 8}}

Here's another difficult one:

enter image description here

(Yes, it is planar, though this particular drawing is not.)

I previously implemented a messy but practically useful method: start with any planar drawing, then use some randomized algorithm that shuffles the coordinates around without allowing the edges to intersect. You can see the results here. This method is clearly not very general, and it has no proper theoretical foundation. I am looking for something better than such heuristic approaches.

Update:

It seems that the problems of the Tutte embedding, i.e. that the ratio of the shortest and longest edge lengths is often very large, can be at least partially remedied by using weighting when computing barycenters.

enter image description here

As a comparison, this is what the unweighted version gives for the same graph:

enter image description here

(Update: The weighted Tutte layout I mention above is now implemented in my IGraph/M package for Mathematica. You can try the interactive example from above in the documentation notebook.)

Szabolcs
  • 1,167
  • If the given graph is on a sphere, one strategy is to use a stereographic projection. – Théophile May 17 '18 at 16:09
  • @Théophile Yes, a planar drawing can always be projected to a sphere, but it's unclear how a simple stereographic projection would improve on a not-very-good plane drawing. What I am looking for is "nice" drawings. Drawing on the sphere is a possible means to this end, not an end in itself. – Szabolcs May 17 '18 at 16:14
  • I'm curious if you know of a "pleasing" drawing of the second difficult graph (i.e. the $2\times6$ grid graph with added diagonals). –  May 17 '18 at 16:37
  • @Rahul This one is not so bad, but I think it could be made better and more symmetric. – Szabolcs May 17 '18 at 16:39
  • @Rahul Here's one that you might call nice, especially if you adjust the coordinates a bit manually. It's symmetric. This is obtained by adding edges to make ti maximal planar, applying a Tutte layout after choosing an appropriate outer face (this is critical and Mathematica chooses an arbitrary one!), then removing the added edges. This is what one would usually get after manual untangling as well. – Szabolcs May 17 '18 at 16:48
  • 1
    Like this – Szabolcs May 17 '18 at 16:51
  • 1
    To put "pleasing" in mathematical context, I will conjecture that you would like (a) the angles between edges to be as large as possible, and (b) the lengths of the edges to be as close to each other as possible. I would imagine that something like this has been studied in the literature – Mike Jun 03 '18 at 01:41

0 Answers0