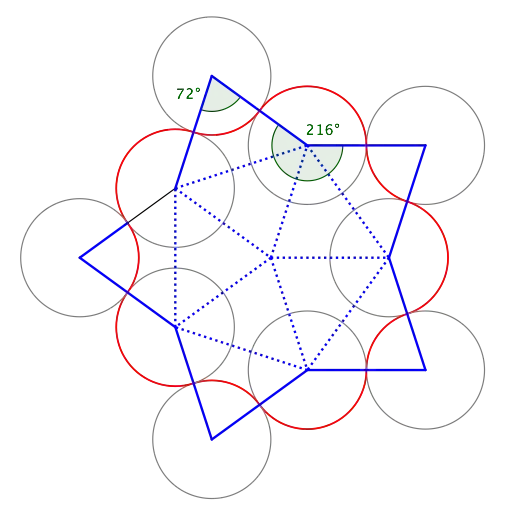
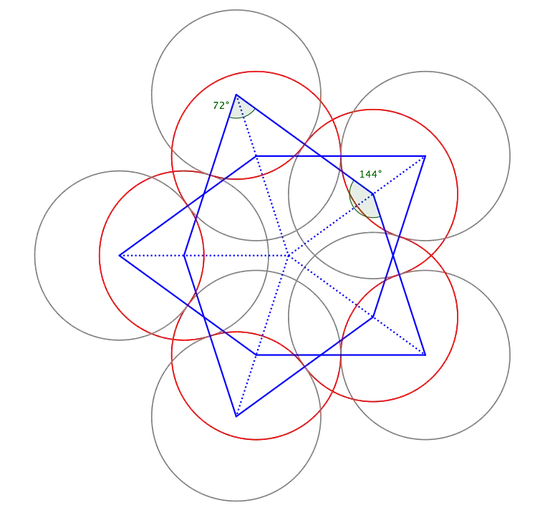
Here's an initial pass that ignores possible complications in the various parameters.
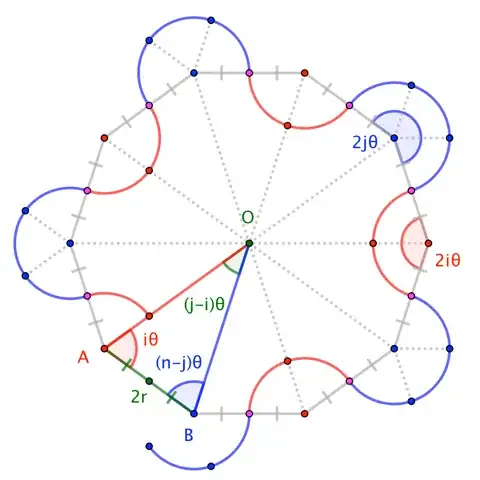
Let the arcs have radius $r$ and angle $2\theta$, where $\theta := \pi/n$. Joining the centers of the arcs creates an cyclic equilateral $2p$-gon (for some $p$) of edge-length $2r$. (The midpoints of the edges are the "inflection points" in the path, where clockwise arcs meet counter-clockwise arc.) The $2p$-gon alternates interior angles $2i\theta$ and exterior angles $2j\theta$. Joining the vertices of the $2p$-gon to its center creates $2p$ congruent triangles, one of which is marked $\triangle AOB$ in the figure.
The area of the path interior is the area of the $2p$-gon, plus the area contributed by sectors bounded by the "$j$" arcs, minus the area contributed by sectors bounded by the "$i$" arcs.
$$2p\;|\triangle AOB| \;+\; p\cdot\frac12r^2\cdot 2j\theta \;-\;
p\cdot\frac12 r^2\cdot 2i\theta
\;=\; 2p\;|\triangle AOB| \;+\; pr^2(j-i)\theta \tag{$\star$}$$
The angles at $A$ and $B$ are half the polygon's interior angles: $\angle A = i\theta$ and $\angle B =(n-j)\theta$. Thus, $\angle O = \pi - \angle A - \angle B = (j-i)\theta$. We see, then, that the number of triangles (ie, the number of sides of the polygon) is $2p = 2\pi/\angle O$, so that $p = n/(j-i)$. (Since $p$ must be a positive integer, we're evidently assuming that $j-i$ is positive, and that it divides $n$.) Thus, $(\star)$ becomes
$$\frac{2n}{j-i}\;|\triangle AOB| \;+\; \pi r^2 \tag{$\star\star$}$$
Let's turn to that triangle. By the Law of Sines,
$$\frac{2r}{\sin(j-i)\theta} = \frac{|OA|}{\sin(n-j)\theta} = \frac{|OB|}{\sin i\theta}$$
Thus,
$$\begin{align}|\triangle AOB| &= \frac12|OA||OB|\sin\angle O \\[4pt]
&=\frac12\cdot \frac{2r \sin(n-j)\theta}{\sin(j-i)\theta} \cdot \frac{2r \sin i\theta}{\sin(j-i)\theta}\;\sin(j-i)\theta \\[4pt]
&=2r^2\;\frac{\sin i\theta \sin(n-j)\theta}{\sin(j-i)\theta}
\end{align}$$
and the area enclosed by the robot path is (maybe)
$$\pi r^2 + \frac{4nr^2}{j-i}\;\frac{\sin \dfrac{\pi}{n} i\; \sin\dfrac{\pi}{n}(n-j)}{\sin\dfrac{\pi}{n}(j-i)} \tag{$\star\star\star$}$$
The interesting part seems to be that the net contribution of the sectors is independent of $i$, $j$, and $n$. That it's specifically the area of one complete circle suggests that a "winding number" component lurks somewhere. Perhaps there's an elegant way to parameterize the path and invoke Green's Theorem. $\square$
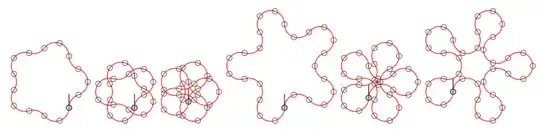 For example, the picture above illustrates the $(1, 2)$-path, $(1, 3)$-path, $(1, 4)$-path,
$(2, 3)$-path, $(2, 4)$-path, and $(3, 4)$-path of a $5$-robot.
For example, the picture above illustrates the $(1, 2)$-path, $(1, 3)$-path, $(1, 4)$-path,
$(2, 3)$-path, $(2, 4)$-path, and $(3, 4)$-path of a $5$-robot.