1

Ive been working on this project for over a week now and its coming due soon, and im in no way going to finish it soon. the project is essentially where we have been assigned 3 "Codes" which form a language, mine are "1111", "101" and "10" and we need to create a finite state acceptor that will accept all strings from this language, with a parity bit on the end (mine is EVEN 1 parity), where if the string has an even number of 1s, the last bit will be 0, and if it has an odd number of 1s the last bit will be 1. i have created 2 Deterministic finite state machines, one to detect even 1 parity, and one to accept all the combinations of those strings. 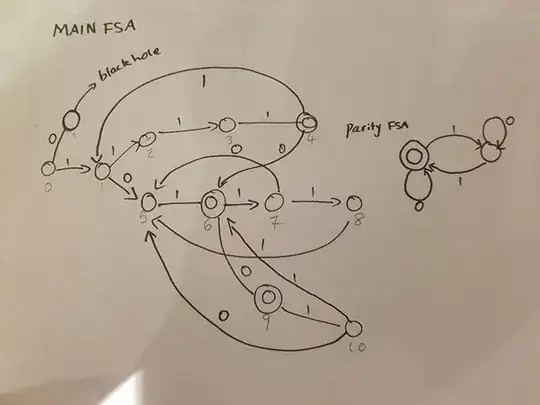my drawings for both are below (any states that do not have 0 or 1 transitions are, those transitions are to a black hole state.) (i dont have reputation 10 on the maths version of the site so i cant post images) two automatons

The 0 transition from state A in the main FSA is so that the FSA will accept the empty string, as the empty string will be assigned a parity bit of 0)

now i need to figure out a way to combine these two together so that i get one FSA which will accept all strings and the parity bit.

the final submission is also in table form, ie:

State 0 transition 1 transition

A … …

B … …

i know that what i need to do is find the intersection of the two languages but im not too sure how to do that. the guideline also gives this clue but if anything it confuses me more:

"Let L denote the regular language (A + B + C)*(0 + 1) and let M denote the collection of all strings that satisfy the parity property. We then need to design a finite state automaton that accepts precisely all the strings of L ∩ M. However, we cannot handle the intersection directly.

The idea is to use De Morgan's law, that L ∩ M = -((-L)+(-M)), where we have used + to denote union. "

any help would be much appreciated, im really stuck on this, and im sure its either gaps in my knowledge or me completely missing something i have to do, but any help would be greatly appreciated.

dtldarek
  • 37,969
  • Related: Intersection of two deterministic finite automata? – dtldarek Apr 26 '18 at 11:27
  • BTW, your automaton seems to accept both $\mathtt{101}$ and $\mathtt{11110}$ which I don't know how to understand (the second either is wrong or has a parity bit, which the first one does not have). – dtldarek Apr 26 '18 at 11:32
  • yeah the main one was my attempt to combine them so i have tried to include the parity bit where i can, but it still accepts strings i dont want it to such as 111100 –  Apr 26 '18 at 11:36
  • Can you create an automaton without any parity bits? – dtldarek Apr 26 '18 at 11:39
  • https://drive.google.com/open?id=1pTYwOVUVE6-H6CayxNHpJRrU5EBZralM –  Apr 26 '18 at 11:43
  • Now, make two copies of that automata, and then each time you follow "0" you go as usual, and each time you follow "1" you change the copy you are in (you go to the same state you should go to, but in the other copy). What language does such an automaton accept? What is the significance of the word being accepted in the lower copy vs. upper copy? (When making pictures, could you orient your screen so that the photo is not rotated?) – dtldarek Apr 26 '18 at 11:59
  • so the main project is to basically take the 3 codes, 1111, 101, 10, and the parity bit, and create an FSA that accepts only the strings that are made up of combinations of these codes, and the parity bit, which in my case is even 1s. ill rename the states in the diagram so its easier to read and explain. but just to clarify , every time i make a 0 transition i stay in the same diagram and every time i make a 1 transition i switch diagrams? if they are the same diagram wont the output be the same ? –  Apr 26 '18 at 12:04
  • https://drive.google.com/open?id=1A8Znddplj8GaoWk2iL85XtgVACL7EAXF here is the updated diagram –  Apr 26 '18 at 12:07
  • Yes, indeed the output would be the same, but notice that the copies are not symmetric due to the initial state (which is only in one copy). The question is, how does the words accepted in the first diagram differ from the words in the second diagram :-) – dtldarek Apr 26 '18 at 12:07
  • i feel like ive completely misunderstood you with this one but is this what you mean haha, and what do you mean by how do they differ from one another, i imagine the first diagram would be set up to support a parity bit of 1, and the second a parity bit of 0?https://drive.google.com/open?id=1cNUztLJPw6HNoD_q4gwduIffkFXN0mR8 –  Apr 26 '18 at 12:17
  • You are missing arrows like $F_1 \to G_2$, but something like this (when correct) would allow you to track the parity of a word. Now you need to add the parity checks and you are done. – dtldarek Apr 26 '18 at 12:26
  • okay so if i did manage to do that correctly how would i implement the parity checks, and would i just remove the inaccessible states ? thank you so much for your help i really appreciate it –  Apr 26 '18 at 12:49
  • ive done this i think it looks about right, where if we are in the left diagram we have an even number of 1s, then on the right side we will have an odd number of 1s, so i guess that means that i would somehow have to implement a 0 parity bit at the left diagram and a 1 parity bit at the right diagram, but how would i go about doing this ?https://drive.google.com/open?id=1KVJzCI6ZZVTdfHiLi0nWaWcYGZjjPIDA –  Apr 26 '18 at 13:07
  • disregard previous, found i missed lots of connections, here is the complete one, now how would i add the paritys?https://drive.google.com/open?id=1cvre23HkaJKsUHLMAmVxhktRsRP-DUcu –  Apr 26 '18 at 13:41
  • If you were constructing a non-deterministic automaton, from each accepting state you could just draw an appropriate arrow "0" or "1" to a new state that would take on the role of being the accepting state. For deterministic automatons you need to find a way to merge that arrows into what you already have and make sure you are adding no new words in the process. And you can prune the unreachable states (but then that would make your copies appear different, and so it might make your automaton seem more complex). – dtldarek Apr 26 '18 at 14:10
  • Okay I think I understand now, so if I was doing it the non deterministic way I would extend a 0 transition from all the accepting States on the left diagram and turn that new state into the accepting state, and the same but with 1s on the other side? –  Apr 26 '18 at 14:16
  • Assuming the old accepting states are not accepting anymore, yes, that would work. – dtldarek Apr 26 '18 at 14:25
  • thank you so much i think i understand now, ill give it a run through and see –  Apr 26 '18 at 14:42
  • so ive created the new one with the new accepting states, but this leaves me with multiple 1 and 0 transitions from the same state so what moves should i make to turn it into a deterministic one ? –  Apr 26 '18 at 14:54
  • OH MY GOD I SOLVED IT YOU ARE AN ABSOLUTE GOD SEND THANK YOU <3 <3 <3 –  Apr 26 '18 at 15:11
  • How can i upvote you you deserve a medal for helping me with this haha –  Apr 26 '18 at 15:17
  • Then, if you are so happy with my help, I would appreciate if you could gather all these comments and steps and edit it into a nice post/answer below (i.e., self-answer your question), so that the next person could also learn something from it (that is, describe not the solution itself, but the process, how to arrive at the solution). – dtldarek Apr 26 '18 at 23:09

2 Answers2

0

we have been assigned 3 "Codes" which form a language, mine are "1111", "101" and "10" and we need to create a finite state acceptor that will accept all strings from this language, with a parity bit on the end (mine is EVEN 1 parity), where if the string has an even number of 1s, the last bit will be 0, and if it has an odd number of 1s the last bit will be 1

So you need to accept the language $\{11110, 1010, 101\}$. This basically consists of two chains of states and a dump state for completeness.

Peter Taylor
  • 13,701
  • I think the OP's intention is a bit different, e.g. $10100$ should be a valid string (i.e., concatenation of codes and then a single parity bit at the very end). – dtldarek Apr 26 '18 at 23:04
0

firstly create a state diagram for the regular expression derived from your language given to you for your FSA, not including the parity bits. for me, my codes were 1111,101,10, and my regular expression then became (1111+101+10)* you can take this and use this website to generate a deterministic finite state acceptor for you to get an idea how its done. http://ivanzuzak.info/noam/webapps/fsm_simulator/

once you have created your deterministic fsa (ie. one without null transitions, as a more basic form ) then you need to check for the parity. to do this, as dtldarek put so well, you need to duplicate your current machine, and have them connect to one another. what i mean by this, is that you have your original machine, with the initial state, that stays the same, but now you have the duplicated one right next to it. (when you are drawing this, only draw the state circles not the transitions between them, we will add this later.) now go through the drawing and rename each state in the original machine from A-Z, and name each state on the new machine A1-z1, so that its easy to see which state you need to transition to. (it also helps if you draw out your duplicated machine right next to it, keeping all the state circles in the same relative positions as the original one.) now what you need to do is draw your transitions based on your parity bit. for me, i had even 1 parity, which meant i needed to track how many 1s i had. now here is the bit i had a bit of trouble getting my head around. what you need to do is let the state transitions help you keep track of your important bits (in my case the 1s). what you need to do is for every 1 transition you go to the same state you would have before, but in the new diagram. for example if you had a 1 transition from A to C, then go from state A, to state C1. and for every 0 transition, stay within the same diagram. when you do this, every time you are in the new diagram on the right, there will be an odd number of 1s, and every time you are in the original diagram there will be an even number of 1s. now we use this to our advantage, and from the accepting states we had before, add a new transition (1 or 0 depending on which side youre on) from the accepting state, to a new accepting state. this means that any string that was accepted previously needs to now have an extra 1 or 0 to be accepted. this will be the parity bit. this needs to be fiddled with a bit, because sometimes you will have used 1 or 0 transitions already for those original accepting states and you wont have any left, which means youll have to find another accepting state to go to.

so for example state C and C1 are accepting states. since state C is in the original diagram, any string that was accepted by C will have an even number of 1s, which satisfies our even 1 parity condition. so now we make C no longer accepting and 0 transition from there to an accepting state, to add the parity bit. its the opposite for C1, where since its in the duplicate, it has an odd number of 1s, so we 1 transition from there to a new accepting state, and remove C1's acceptance

i hope that helps a bit !