Lax-Wendroff method for linear advection - Matlab code

Question

$$ {\bf u}^{n+1} = {\bf u}^{n} - \frac{\Delta t}{2 \Delta x} {\bf c}.^*({\bf D}_{\bf x}{\bf u}^n) + \frac{\Delta t^2}{2 \Delta x^2} {\bf c}^2.^*({\bf D}_{\bf x x}{\bf u}^n) + \frac{\Delta t^2}{8 \Delta x^2} {\bf c}.^*({\bf D}_{\bf x}{\bf c}).^*({\bf D}_{\bf x}{\bf u}^n) , $$ where ${\bf c}^2$ is the element-wise square of the vector ${\bf c}$. You should state clearly what the vectors ${\bf u}^n$ and ${\bf c}$ and matrices ${\bf D}_{\bf x}$ and ${\bf D}_{\bf xx}$ are.

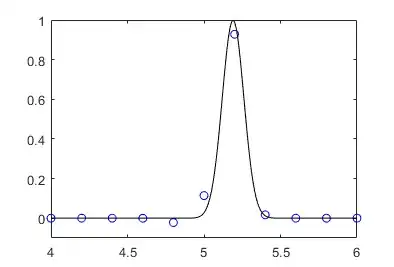
Take $x \in [0,10]$, $u(0,t) = u(10,t) = 0$, $c = 1/5$ and initial condition $u(x,0) = e^{-100 (x-5)^2}$. Using MATLAB, numerically implement the Lax-Wendroff scheme for $N = 50$ and plot the solution at $t = 1$. You are required to choose a time step such that the scheme is numerically stable. Discuss your reasoning for the time step you chose.

I am trying to code a solution for this PDE $ u_t +c(x)u_x = 0 $ in Matlab using the above scheme, However I am really unsure about how to define my boundary conditions in Matlab. Since the boundary equals zero, but not sure if i start at $j=1$ or $j = 0$, which would mean i have to introduce ghost pints, which i wasn't been given, so i am thinking i don't need to this?

Also Matlab says my matrix dimensions dont agree, but i cant seem to fix this? Can anyone see the error?

My code so far,

 Nx = 100;

 x  = linspace(0,10,Nx);

 dx = 10/Nx;

 tmax = 1;

 dt = dx/50;  % ensure stability

 R = round(tmax/dt);
 e = ones(Nx,1);

 Dx  = spdiags([-e e],[-1 1],Nx,Nx);

 Dxx = spdiags([e,-2*e,e],[-1 1], Nx, Nx);

 Dx(1,2) = 0; 
 Dx(Nx,Nx-1) = 0; % change entries determined by BCs

 c = 1/5*ones(Nx,1);

 p  = 0.2*dt/dx;

 % initial data
 u = zeros(Nx,1);

 % initial condition
 for i=1:11
     u(:,1,i)=exp(-100*(x-0.5).^2)';
 end

 for n = 2:R
     u(:,n+1)=u(:,n) - 1\2*p*c.*Dx.*u(:,u) + 1/2*p^2*c^2.*Dxx*u(:,u)  + 1/8*p^2*c^2.*Dx*u(:,u);
 end

 plot(x,u(:,),'-or');

 xlabel('x');
 ylabel('u');
 title('Solution at t = 1');

Answer 1

We refer to this post for notations. The spatial discretization is $x_j = j \Delta x$ for $j = 0,\dots , N$, where $\Delta x = 10/N$. Since $u_0^n \approx u(0,t)$ and $u_N^n \approx u(10,t)$ are known, the vector of unknowns ${\bf u}^n = (u_1^n , \dots , u_{N-1}^n)^\top$ is of size $N-1$. Moreover, since $u_0^n$ and $u_N^n$ equal zero, they do not appear in the right-hand side of the scheme at the lines corresponding to the computation of $u_1^{n+1}$ and $u_{N-1}^{n+1}$. Lastly, let us introduce the vector ${\bf c} = (c_1, \dots , c_{N-1})^\top$. Thus, using MATLAB's matrix notation, $$ {\bf u}^{n+1} = {\bf u}^{n} - \frac{\Delta t}{2 \Delta x} {\bf c}.^*({\bf D}_{\bf x}{\bf u}^n) + \frac{\Delta t^2}{2 \Delta x^2} {\bf c}^2.^*({\bf D}_{\bf x x}{\bf u}^n) + \frac{\Delta t^2}{8 \Delta x^2} {\bf c}.^*({\bf D}_{\bf x}{\bf c}).^*({\bf D}_{\bf x}{\bf u}^n) , $$ where ${\bf D}_{\bf x}$ and ${\bf D}_{\bf xx}$ are the $({N-1})\times ({N-1})$ matrices given by $$ {\bf D}_{\bf x} = \left( \begin{array}{cccc} 0 & 1 & & \\ -1 & \ddots & \ddots & \\ & \ddots & \ddots & 1 \\ & & -1 & 0 \\ \end{array} \right) , \quad {\bf D}_{\bf xx} = \left( \begin{array}{cccc} -2 & 1 & & \\ 1 & \ddots & \ddots & \\ & \ddots & \ddots & 1 \\ & & 1 & -2 \\ \end{array} \right) . $$ Here is a corresponding code in MATLAB syntax:

% parameters
N = 50;
CFL = 0.95; % Courant number
c = 0.2*ones(N-1,1);
tend = 1;

dx = 10/N;
x = linspace(dx,10-dx,N-1)';
dt = CFL*dx/max(c);
c2 = c.^2;

One = ones(1,N-2);
Dx  = diag(One,1)              - diag(One,-1);
Dxx = diag(One,1) - 2*eye(N-1) + diag(One,-1);

% initialization
t = 0;
u0 = @(x) exp(-100 * (x-5).^2);
u = u0(x);

% iterations
while (t+dt)<tend
    u = u - 0.5*dt/dx * c.*(Dx*u) + 0.5*(dt/dx)^2 * c2.*(Dxx*u) ...
      + 0.125*(dt/dx)^2 * c.*(Dx*c).*(Dx*u);
    t = t + dt;
end

% graphics
figure;
plot(x,u,'bo');
hold on
if norm(diff(c))<1e-14
    plot((0:0.01:10),u0((0:0.01:10) - c(1)*t),'k-');
end
xlim([0 10]);
ylim([-0.1 1]);

Since the speed $c = 1/5$ is constant, the result at $t=1$ should be a translation of the initial data by $ct \approx 0.2$, i.e. $u(x,t) = u(x-ct,0)$. Despite the fact that $N=50$ is not large enough for a good resolution, this analytical result (black solid line) is coherent with the numerical result (blue circles):

Here, the Courant number is set to $0.95$. As shows von Neumann analysis, stability is obtained for Courant numbers smaller than one. The Courant number should be as large as possible so as to increase $\Delta t$ and reduce the number of iterations in time. Moreover, numerical diffusion increases when the Courant number diminishes.

Answer 2

My revised code was not working. It seemed to not iterate through loop and only plot initial condition... Here is a version debugged by Harry49 (it's working now):

% setup and  parameters
Nx = 50;  % number of mesh points
dx = 10/Nx; % spactial mesh 
Tend =1;% solve from t=0..tmax

c = 0.2*ones(Nx-1,1); %  vector  of ones , size Nx-1
cfl=0.95;
dt = cfl*dx/max(c);% time step
R = round(Tend/dt); %  number of timesteps
x = linspace(dx,10-dx,Nx-1);% create spatial coordinates vector for plots

% set up differentiation matrices 
e = ones(Nx-1,1); % vector of ones of same size x
Dx  =(spdiags([-e e],[-1 1],Nx-1,Nx-1)); % 1st order matrix
Dxx = (spdiags([e -2*e e], [-1 0 1], Nx-1,Nx-1)); % 2nd order matrix

% initialization and initial conditions,   u = zero at boundaries 
u = exp(-100 * (x-5).^2)';

for n = 1:R % iteratre, step in time
   u(:,n+1) = u(:,n) - 0.5*dt/dx * c.*(Dx*u(:,n)) + 0.5*(dt/dx)^2 * c.^2.*(Dxx*u(:,n)) ...
      + 0.125*(dt/dx)^2 * c.*(Dx*c).*(Dx*u(:,n));
end

(plot(x,u(:,R+1),'o - r'));xlabel('x'); ylabel('u'); title('Solution @ t=1')